Computer Architecture

CSAPP CacheLab

CacheLab分析及解题(含代码实现)

Posted by Kylin on May 26, 2019

CSAPP CacheLab (CMU)

实验环境：Ubuntu 18.04，ThinkStation P500

Cache Lab 简介

  • 实验共有两个部分，Part A 和 Part B，主要目的是为加深对 CPU Cache Memory 的理解。

  • Part A要求使用C language实现一个Cache模拟器，主要要求了解Cache的寻址方式，以及 LRU(Least Recently Used) 算法的工作方式，测试是以动态分析工具 valgrind 为基础，对照标准程序的 Miss，Hit，Evict 给分。

  • Part B要求实现一个矩阵转置的函数，用以测试 32x32，64x64，61x67的矩阵样例，要求Cache在满足参数 (1024B，s=5，E=1，b=5) 的条件下，Miss满足测试标准。

    (细节参考Cachelab Description.pdf )

Part A

问题分析

  • Cache模拟的实现的问题主要集中在两个方面：
    • Cache的数据结构（如果采用抽象的数据结构可以略过这个点）
    • Cache的寻址方式

这两个问题都可以由 CSAPP 6.4.3 来解答，即组关联 Cache 的结构

​ CASPP插图

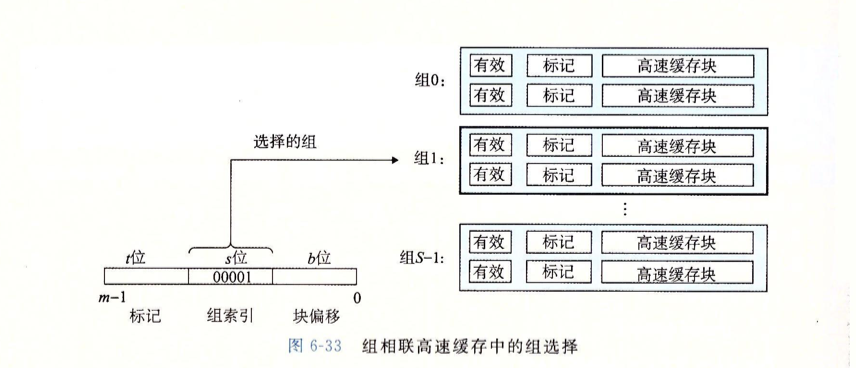
  • 由这张图可以得到以下几点：
    • 左下角为地址格式 (在实验中即64位)，中间的s位组索引及我们的 Terminal参数”-s”，其用来索引组号，因此共用 $S=2^s$ 组。
    • 在用组索引确定了具体组之后，用地址中的前t位（具体位数由公式 $t=m-s-b$ 间接计算) 与Cache 中的标记位做比对，如果存在 (有匹配成功的行) 则 Hit，反之 Miss，根据指令类型与Cache是否满确定是否有进一步操作（如 Evict）。
    • 地址的最后b位 (即 Termial 参数”-b”) 块偏移表示块的大小，其用于索引目标块（行）中的缓存，共可以索引 $B=2^b$ 位。
    • $t=m-s-b$ 中的 $m$ 即指令的位数。

具体实现

  • 我们用一个 Struct 嵌套的层级结构来表示 Cache
| struct cache
├── struct cacheSet
    ├── struct setLine
        ├── int valid
        ├── int tag
        ├── char* block
        └── (help) int timeStamp

timeStamp 用来确定在 LRU 下要 Evict 的缓存

具体代码实现如下：

typedef struct{
	// Three fundamental parameters in perline 
	int valid;
	unsigned long long tag;
	char *block;
	// choose which to evict in LRU
	int timeStamp;
} setLine;

//set struct
typedef struct{
	setLine *lines;
} cacheSet;

//cache struct
typedef struct{
	cacheSet *sets;
} cache;
  • 用一个结构体 cachePara 来储存 Cache 参数及最终结果（Miss, Hit, Evict）
typedef struct{
	int s;//Number of set index bits (S = 2^s is the number of sets)
    int S;//S=2^s
    int b;//Number of block bits (B = 2^b is the block size)
    int B;//B=2^b
    int E;//Associativity (number of lines per set)
    int verbosity;//Optional verbose flag that displays trace info
    
    //LRU output
    int hitNum;
    int missNum;
    int evictionNum;
} cachePara;
  • 主函数 main() 主要负责以下两个个部分：
    • 利用”getopt.h”从 terminal 读取参数初始化结构体 CachePara
    • 从trace文件读取指令, 同时调取函数Simulate进行模拟
int main(int argc, char** argv){
	//init cache structure
	cache LRUcache;
    cachePara parameters;
    parameters.verbosity=0;

    //use getopt.h to read data from terminal, store them in parameters(1)
    char input;
    char *trace;
    while( (input=getopt(argc,argv,"s:E:b:t:vh")) != -1){
        switch(input){
        case 's':
            parameters.s = atoi(optarg);
            break;
        case 'E':
            parameters.E = atoi(optarg);
            break;
        case 'b':
           parameters.b = atoi(optarg);
            break;
        case 't':
            trace = optarg;
            break;
        case 'v':
            parameters.verbosity = 1;
            break;
        // print parameter prototype
        case 'h':
            printUsage();
            exit(0);
        default:
            printUsage();
            exit(-1);
        }
    }

    //init parameters(2)
    parameters.S = pow(2.0,parameters.s);
    parameters.B = pow(2.0,parameters.b);
    parameters.missNum = 0;
    parameters.hitNum = 0;
    parameters.evictionNum = 0;

    //cache init
    LRUcache = initCache(parameters);

    //imput trace file while simulation
    char command;
    int size;
    unsigned long long address;
    FILE *file;
    file=fopen(trace,"r");
    while(fscanf(file," %c %llx,%d",&command,&address,&size)==3){
    	switch(command){
    		case 'I':
                break;
    		case 'L': //Load
                parameters = simulate(LRUcache, parameters, address);
                break;
            case 'S': //Store
                parameters = simulate(LRUcache, parameters, address);
                break;
            case 'M': //Modify
                parameters = simulate(LRUcache, parameters, address);
                parameters = simulate(LRUcache, parameters, address);	
                break;
            default: //ignore 'I'
                break;
    	}
    }
    printSummary(parameters.hitNum,parameters.missNum,parameters.evictionNum);
    fclose(file);

    return 0;
}
  • 我们区别I、M、S指令的问题放在Main()的层级上解决，即Simulate()函数只负责访问Cache内的目标内容，若存在则Hit；若不存在，则 Evict (若CacheSet已满) 再 Load 进入 Cache。之后 Simulate() 将结果储存在 CachePara 内。

Simulate()函数如下：

cachePara simulate(cache currentCache, cachePara parameters, unsigned long long address){
    //get the tag
	int tagSize = 64-(parameters.b + parameters.s); //64 bit system
    unsigned long long tag = address >> (parameters.s + parameters.b);
    //get the set index
    unsigned long long tmp = address << (tagSize);
    unsigned long long setIndex = tmp >> (tagSize + parameters.b);
    cacheSet set = currentCache.sets[setIndex];
    
    int flag=1;//1 to hit, 0 not;

    //simulation hit
    for(int i=0;i<parameters.E;i++){
    	setLine currentLine=set.lines[i];
    	if(checkHit(currentLine,tag)==1){
    		parameters.hitNum++;
            flag=0;
            int tail=checkTail(set, parameters);
            set.lines[i].timeStamp = set.lines[tail].timeStamp+1;
    	}
    }

    //simulation miss load
    if(flag && checkFull(set,parameters)){
    	parameters.missNum++;
    	int loadIndex= checkLoad(set,parameters);
    	set.lines[loadIndex].valid=1;
    	set.lines[loadIndex].tag=tag;
    	int tail=checkTail(set,parameters);
    	set.lines[loadIndex].timeStamp=set.lines[tail].timeStamp+1;
    }
    else if(flag){
        parameters.missNum++;
        parameters.evictionNum++;
        int evictIndex= checkEvict(set,parameters);
        set.lines[evictIndex].valid=1;
        set.lines[evictIndex].tag=tag;
        int tail= checkTail(set,parameters);
    	set.lines[evictIndex].timeStamp=set.lines[tail].timeStamp+1;
    }
    return parameters;
}
  • 一些 Simulate() 内的辅助函数 (只给出声明)
int checkHit(setLine line, unsigned long long tag);
int checkFull(cacheSet set, cachePara parameters);
int checkTail(cacheSet set, cachePara parameters);
int checkLoad(cacheSet set, cachePara parameters);
int checkEvict(cacheSet set, cachePara parameters);

(* 完整代码见文末)

测试结果

执行测试 test-sicm 结果如下：

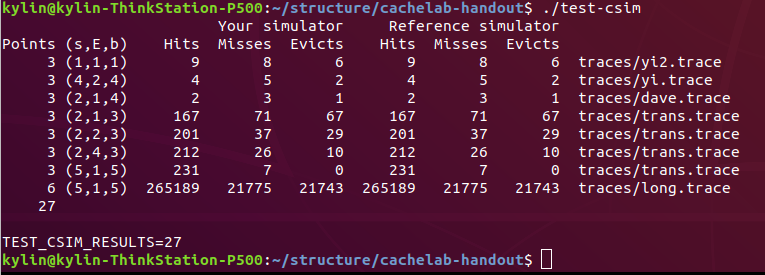
Part B

  • 该部分要求实现一个Cache友好的矩阵转置函数，使Cache Miss次数满足如下条件：
    • 32 × 32: 8 points if M < 300, 0 points if M > 600.
    • 64 ×64: 8 points if M < 1, 300, 0 points if M > 2, 000.
    • 61 ×67: 10 points if M < 2, 000, 0 points if M > 3, 000.

问题分析

  • 给定 CacheSize = 1024B，s=5，E=1，b=5。这意味着这是一个直接映射关联 (即单路组关联)，而且这个 Cache 每次可以容纳一个Matrix的前8行。
  • 将矩阵分成合适大小的块分别求转置可以减少Miss。
  • 鉴于可使用变量不超过12个，我们尽量不使用另外的函数调用。而且，在矩阵分块后，块循环与元素循环共需要4个变量，初次之外我们在定义8个临时变量 $tmp1$至 $tmp8$ 。

变量定义如下

//variables init
    int row, col;
    int rowCheck, colCheck;
    int tmp1,tmp2,tmp3,tmp4,tmp5,tmp6,tmp7,tmp8; //temprary variables for exchange two values

具体实现

  • 32 x 32

用 8x8 的分块即可实现，但要注意对角线上的元素(此时Matrix A和Matrix B索引到同一个CacheSet，会发生冲突) 要单独拿出来讨论。（代码中仅以N来区别三个测试）

if (N == 32){
		for(rowCheck = 0; rowCheck < N; rowCheck += 8)
        {
            for(colCheck = 0; colCheck < N; colCheck += 8)
            {
                for(row = rowCheck; row < rowCheck + 8; row++)
                {
                    for(col = colCheck; col < colCheck + 8; col++)
                    {
                        if(row != col)
                        {
                            B[col][row] = A[row][col];
                        }
                        
                        else
                        {
                            tmp1 = A[row][col];
                            tmp2 = row;
                        }
                    }
                    if (rowCheck == colCheck)
                    {
                        B[tmp2][tmp2] = tmp1;
                    }
                }
            }
        }
	}
  • 61 x 67

由于测试要求比较宽松，而且不规则的matrix不能找到比较显然的规律看出来间隔多少可以填满一个Cache，所以尝试分块大小为16，可以实现要求的2000以下的MIss。

for(rowCheck = 0; rowCheck < N; rowCheck += 16)
        {
            for(colCheck = 0; colCheck < M; colCheck += 16)
            {
                for(row = rowCheck; (row < N) && (row < rowCheck + 16); row++)
                {
                    for(col = colCheck; (col < M) && (col < colCheck + 16); col++)
                    {
                        if(row != col)
                        {
                            B[col][row] = A[row][col];
                        }
                        
                        else
                        {
                            tmp1 = A[row][col];
                            tmp2 = row;
                        }
                    }
                    if (rowCheck == colCheck)
                    {
                        B[tmp2][tmp2] = tmp1;
                    }
                }
            }
        }
  • 64 x 64

该情况考虑使用 8x8 大小的分块，但是先尽量把Matrix A中尽量多的元素 (4x4的小分块移入Matrix B)，之后再在Matrix B中进行元素位置的重新调配。

else if (N == 64){
        for(colCheck = 0; colCheck < N; colCheck += 8)
        {
            for(rowCheck = 0; rowCheck < N; rowCheck += 8)
            {
            	for(row=rowCheck;row<rowCheck+4;++row)
            	{
                    tmp1=A[row][colCheck];tmp2=A[row][colCheck+1];tmp3=A[row][colCheck+2];tmp4=A[row][colCheck+3];
                    tmp5=A[row][colCheck+4];tmp6=A[row][colCheck+5];tmp7=A[row][colCheck+6];tmp8=A[row][colCheck+7];

                    B[colCheck][row]=tmp1;B[colCheck][row+4]=tmp5;B[colCheck+1][row]=tmp2;B[colCheck+1][row+4]=tmp6;
                    B[colCheck+2][row]=tmp3;B[colCheck+2][row+4]=tmp7;B[colCheck+3][row]=tmp4;B[colCheck+3][row+4]=tmp8;
                }
                for(col=colCheck;col<colCheck+4;++col)
                {
                    tmp1=B[col][rowCheck+4];tmp2=B[col][rowCheck+5];tmp3=B[col][rowCheck+6];tmp4=B[col][rowCheck+7];
                    tmp5=A[rowCheck+4][col];tmp6=A[rowCheck+5][col];tmp7=A[rowCheck+6][col];tmp8=A[rowCheck+7][col];
       
                    B[col][rowCheck+4]=tmp5;B[col][rowCheck+5]=tmp6;B[col][rowCheck+6]=tmp7;B[col][rowCheck+7]=tmp8;
                    B[col+4][rowCheck]=tmp1;B[col+4][rowCheck+1]=tmp2;B[col+4][rowCheck+2]=tmp3;B[col+4][rowCheck+3]=tmp4;
                }
                for(col=colCheck+4;col<colCheck+8;++col)
                {
                    tmp1=A[rowCheck+4][col];tmp2=A[rowCheck+5][col];tmp3=A[rowCheck+6][col];tmp4=A[rowCheck+7][col];
                
                    B[col][rowCheck+4]=tmp1;B[col][rowCheck+5]=tmp2;B[col][rowCheck+6]=tmp3;B[col][rowCheck+7]=tmp4;
                }
            }
        }
    }

(* 完整代码见文末)

测试结果

执行测试 test-trans 32 x 32 结果如下：

执行测试 test-trans 64 x 64 结果如下：

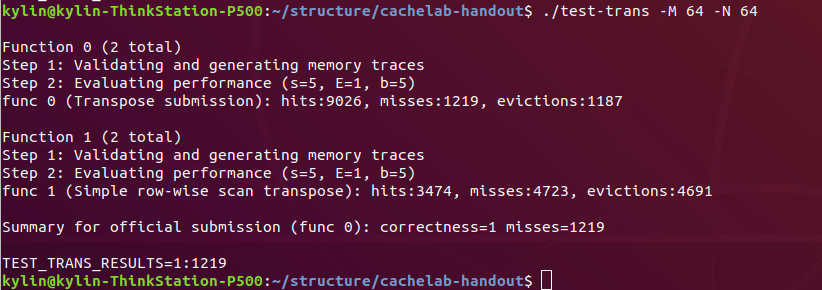
执行测试 test-trans 61 x 67 结果如下：

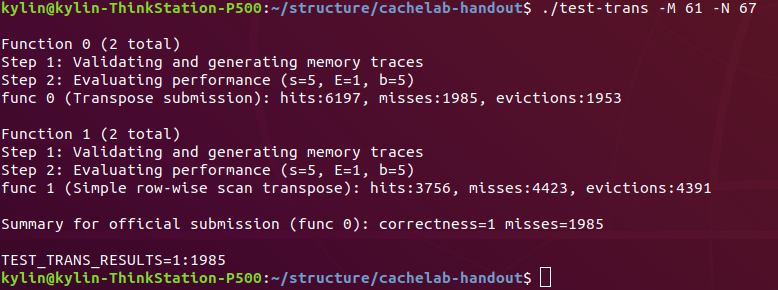
完整代码

参考我的GitHub：https://github.com/KylinC/CSAPP-Labs

CATALOG
    FEATURED TAGS
    From Bohemia Linux Git Cloud Computer Architecture Database machine learning paper software coding quant Object Detection job programming Competition lecture nlp competition llmsys
    FRIENDS