贝叶斯神经网络(BNN)及变分证据下界(VELOB)
对于机器学习领域最简单的神经网络(NN)结构,我们知道的事实是:一旦模型的网络结构(在假设全连接的基础上,是一个表示各层神经元数量的一维向量 T = t_1, t_2, \dots t_n)、传播权重及偏置(传播权重为一组矩阵 W,偏置为b,这里将标准化处理视为单独层)确定,那么模型就会输出确定的结果。一个简单的事实是,如果在工程中选取相同的随机种子生成对应的初始化权重,再用同质同序的训练数据加以训练,在确定性的反向传播算法下,我们得到的是一个完全相同的模型!我们知道,这与实际的应用场合是及其不相同的,因为这样的模型对于任意的输入都会给出一个输出,哪怕这个输入是极不合理的。而从另一方面看,我们知道机器学习在不可解释性上一直为人所诟病,而对于这里的例子,我们不可能把输出单纯看作概率(哪怕经过softmax)。这里给出一个简单的例子,对于Mnist手写数字分类的NN网络中,我们选择 28\times 28 的输入层(图片大小),选择 10\times 1 的输出层(一共只用0~9的分类),那么对于输入的一张”猫”的图像,它仍然会判断出它是 0~9 中的哪个数字而不给出原因(这是及其荒谬的)。而对于人来说,哪怕一只猫像一个数字(实际中可能性不大),也会有诸如 不像/有点像/像/非常像 这类概率划的表述。我曾在这方面研究过,利用反向传播(BP)尝试绘制固定标签的图像,得到以下结果:

(可以参考我的代码以及自己实现: https://github.com/KylinC/Number-Recognization)
这些是 0~9 进行反向回传后的图像,如果不提供 0~9 是从左往右、从上到下的信息的话,我们几乎难以知道对应数字的标签是什么。这意味着普通的NN结构之时在以上的标准 Tempalte 上进行比较,和相似度最高的图片标签进行绑定,本质上和KNN中关于欧式距离的聚类是一致的,不过这个聚类由于隐藏层矩阵无法被直观性的感知。
那么,我们是否可以利用概率论的方法随机化机器学习过程?答案是肯定的,概率统计及随机过程(MCMC)的方法在机器学习上有着很多应用,小到SHUFFLE和随机梯度下降都显示着概率统计的方法。本文中主要讨论的是贝叶斯方法(BNN)及变分证据下界(VELOB)在神经网络方面的应用,并同样在 Mnist 上进行测试,说明该方法的有效性。
首先,我们把问题进行形式化,我们假设 X 是我们的观察(ML问题中的数据),而 Z 是隐变量(ML问题中的模型参数,根据上文关于NN的陈述,完整的NN参数集合即确定唯一的模型)。在这里显而易见的是,Z 分布是确定 X 分布的(下文我们用小写 z, x 表示概率密度)。隐变量的后验概率分布(posterior distribution)可以通过贝叶斯公式得到:

其中,p(Z|X) 是隐变量在数据分布下的后验概率分布(posterior distribution),也就是机器要学习的目标。p(X|Z) 是数据在隐变量确定时的采样似然分布(likelihood distribution), p(Z) 即隐变量先验概率分布,p(X) 即为证据。
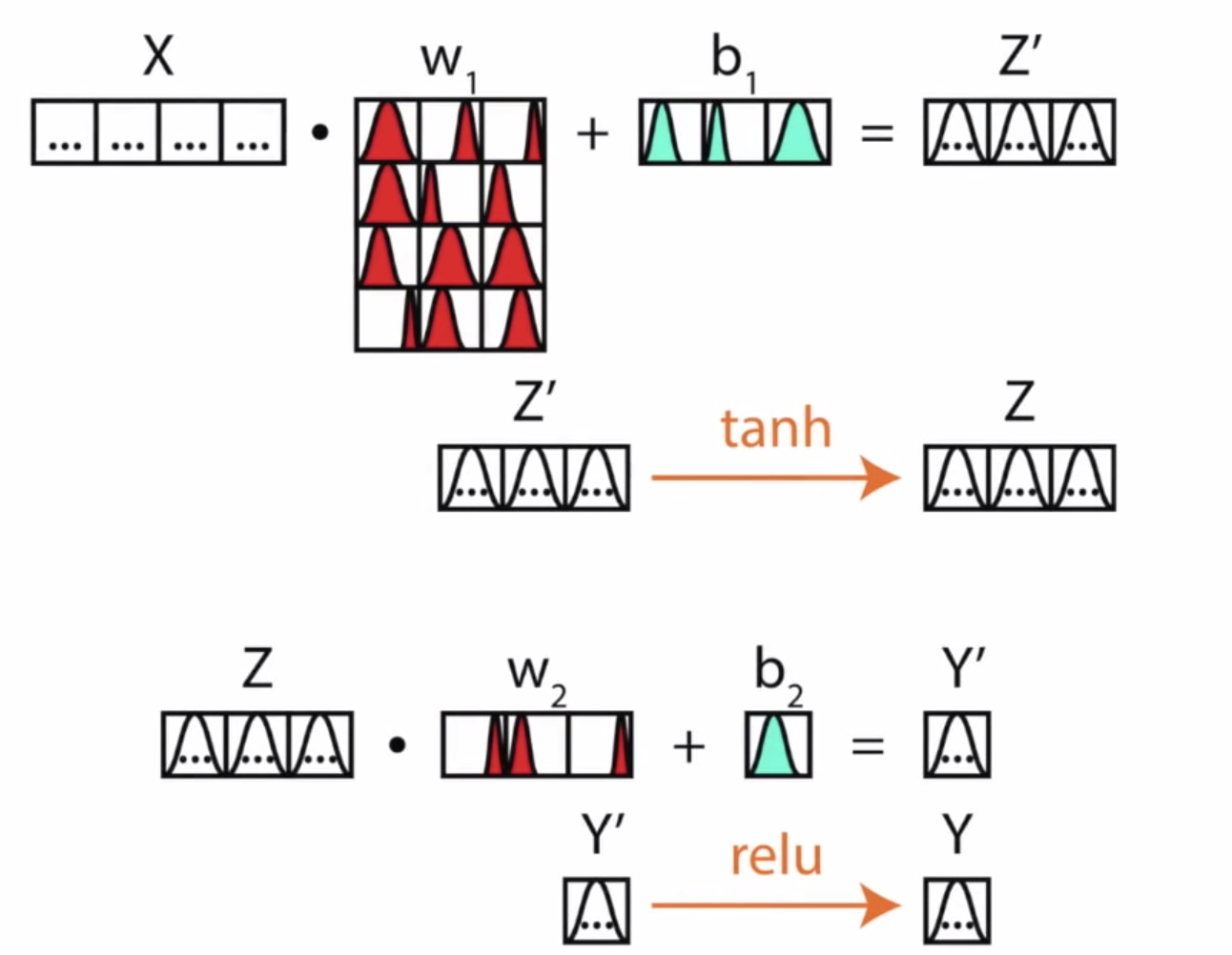
在回到我们关于NN的描述上,我们对于NN从一个确定性模型变为一个概率模型最直观的解决方案是把其中的每一个确定权重和确定值(中间层中的向量)变为一个概率分布,如图所示:
(图片来自文章)
我们可以看到,在这个网络结构中,每一个值都是一个分布。在正向传播进行预测时,我们采用的是多次Sample(最大似然)进行某个确定值的计算。事实上,我们确实是使用这样的网络进行计算的,即使最终的输出在经过最大似然的确定化后与普通NN并没有任何区别,不过取样的分布函数却使得这个机器学习过程可以有可解释的空间(可以设定置信度,即超过某个阈值才能进行判断,这与人的直观十分相似),这样的话,相信在给一张”猫”的图像到0~9点Mnist网络后,网络就可以在置信度合理的情况下,拒绝判断,给出”这张图片不是0~9点图片”这样非编程性(确定性)的答案。
那么贝叶斯化的NN中概率分布如何进行确定,就要参考上文给出的贝叶斯公式,其中 p(X|Z), p(Z) 两项是容易求解的,即参数确定下数据的采样以及参数的采样,这两项只需在多次前向传播(feed-forward)中即可确定,而唯一不确定的是分母中的积分项,由全概率我们可以做如下推导:

这表示,在批处理中(如果不进行批处理,就视作一个批只有一个数据点),我们如果对一个Batch的数据进行前向传播,需要知道所有数据集(即N个Batch对模型的取样概率),而N的数量是巨大的,使得直接采用每个Batch进行独立计算不能接受。这使得我们提出变分傅立叶方法(Variational Bayesian,VB)进行这一全概率项的近似计算,其中使用的重要概念是变分证据下界(variational evidence lower bound,VELBO or ELBO),我们之后会看到其实这一模拟计算过程是确定性的,因为它的本质是用另一个函数的拟合,而把相似度(KL熵)加入到置信判断中。
首先先看 p(X) 这一项该如何与ELBO进行关联,假设任意拟合函数为 q(Z), 则有:

最后我们记 ELBO 为变分下界(variational lower bound)。
之后我们给出拟合函数的KL熵(Kullback-Leibler divergence)与 L(lower bound)的关系推导:
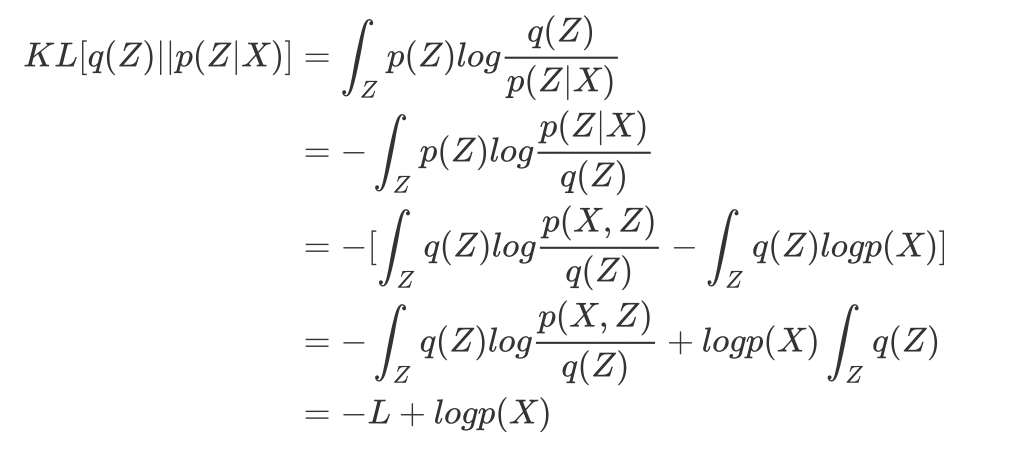
在这里,我们用到了 \int_Zq(Z)=1 的结论,这是由于拟合函数也具有标准性决定的。
由KL熵始终大于0我们可以推断出,当且仅当 L=logp(X) 时,KL熵为0,此时边缘函数 logp(X) 等于变分下界,p(X,Z) 和 p(Z) 无限接近。有了这点,我们在进行全概率项计算的时候,就可以将函数 q(X) 朝着变分下界进行优化,由于边缘函数不变(每一次取样的数据集子集是确定的),所以就是朝着变分下界最大化的方向进行优化。
这里给出一张以上近似的可视化:

(图片来源:https://medium.com/neuralspace/probabilistic-deep-learning-bayes-by-backprop-c4a3de0d9743)
代码实现
解决了贝叶斯公式中 p(X) 项的计算,我们的贝叶斯化神经网络即有了完整的实现理论基础,下面我们进行一些测试:
我们利用pytorch以及pyro(pytorch的一个附属库,可以支持把torch.tensor随机化)在Mnist搭建了基于ELOB的贝叶斯化神经网络,在Mnist手写数字识别10000测试集上取得96%的预测准确率(10个训练轮次),更重要的是,我们在一些数据的可解释性上取得了突破。
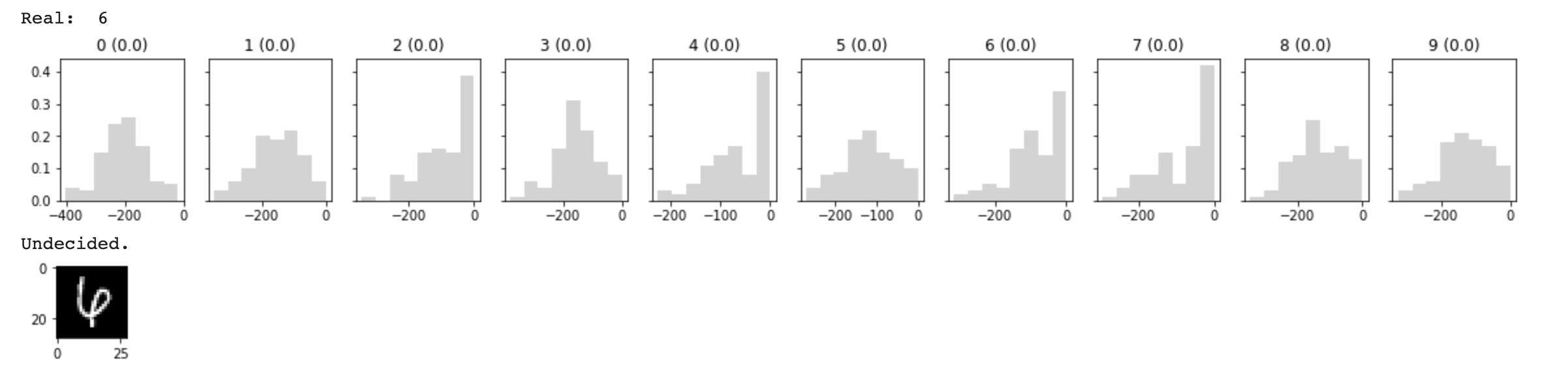
比如对于如下的0和6,对于人类来说,其实也很难判断这个手写数字是什么(图一的0像6,图二的6像4),而我们的BNN学会了拒绝判断,对于图二,其实BNN很想判断它是2,4,6,7,但是由于分布不接近0(没有到达置信阈值),所以没有给出判断。(关于为什么置信分布要接近0参考上文边缘函数 logp(X) 的推导。

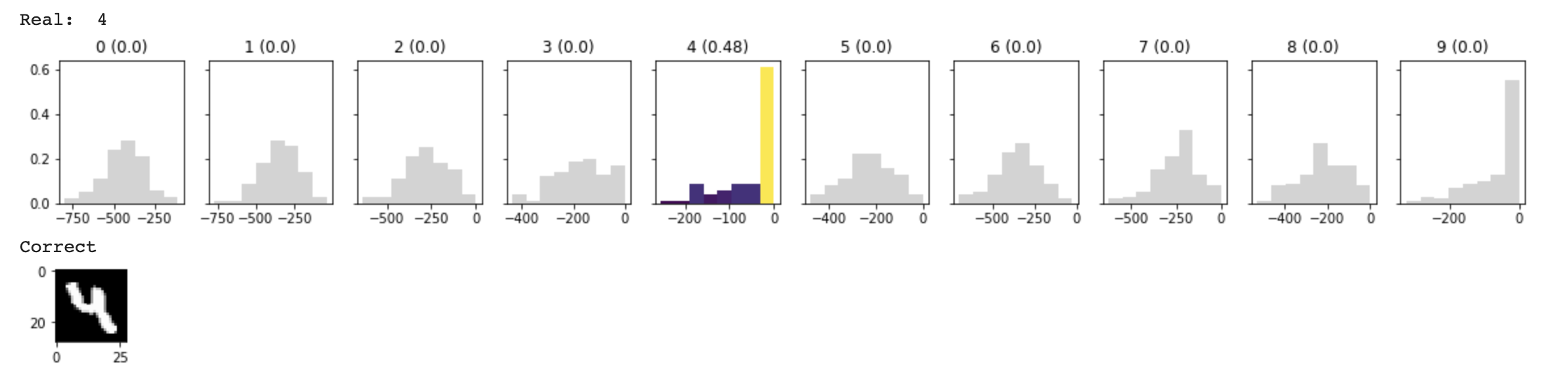
再看这张4,我们发现它的置信分布并没有完全在0附近,这说明它是不太肯定这是4的,看图片我们肯定BNN这一判断,因为人类也很难准确判断。
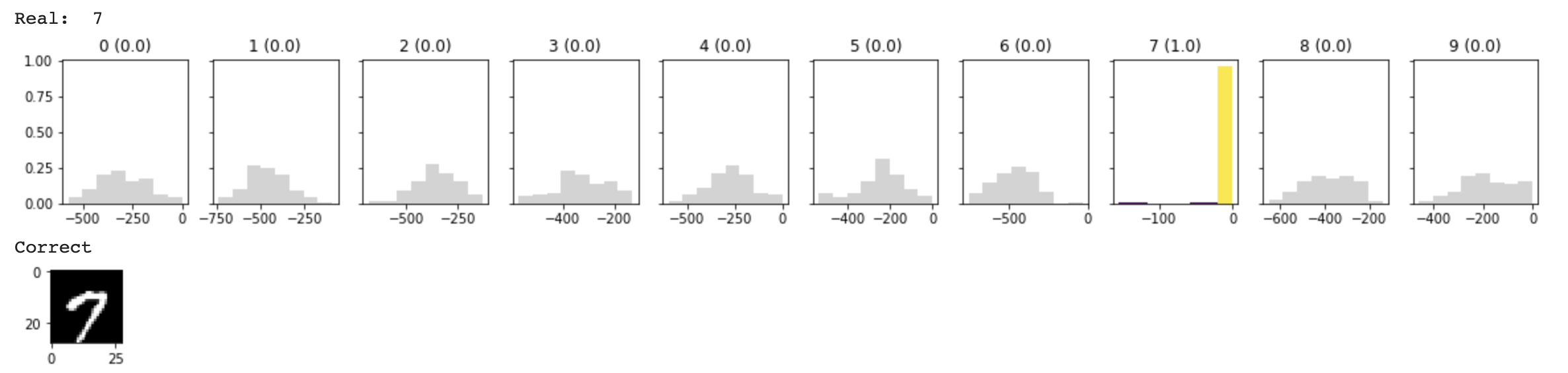
给出一张特征明显的7,我们发现BNN给出了相当确定的答复。
本文给出了贝叶斯公式用于变分证据下界(VELOB)的构造以及实现了贝叶斯神经网络,实现代码:https://github.com/KylinC/BCNN。