Tree-based Model

Classification And Regression Tree (CART, supervised)

Decision Tree for Classification

Ad：

a classification tree learns a sequence of if-else questions about individual features
able to capture non-linear relationships between features and labels
trees don’t require the features to be on the same scale through standardization
决策树模型不需要标准化，因为每一个节点的分裂点 (sp) 的分裂缩放位置 (比例) 是固定的

DisAd：

只能产生正价决策边界（orthogonal decision boundaries）
对于训练集敏感（一条数据改变树结构）
Unconstrained CARTs may overfit the train set

# import Desicion Tree
from sklearn.tree import DecisionTreeClassifier
# import train_test_split
from sklearn.model_selection import train_test_split
# Import accuracy_score
from sklarn.metrics import accuracy_score

# 分割数据集，以获得模型性能的无偏估计, stratify=y使得训练集和测试集有相同比例的类标签
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,stratify=y,random_state=1)

# 实例化一棵树
dt = DecisionTreeClassifier(max_depth=2, random_state=1)

# fit dt to training set
dt.fit(X_train,y_train)

# predict the test set label
y_pred = dt.predict(X_test)
# evaluate the test_set accuracy
accuracy_score(y_test,y_pred)

decision region & decision boundary

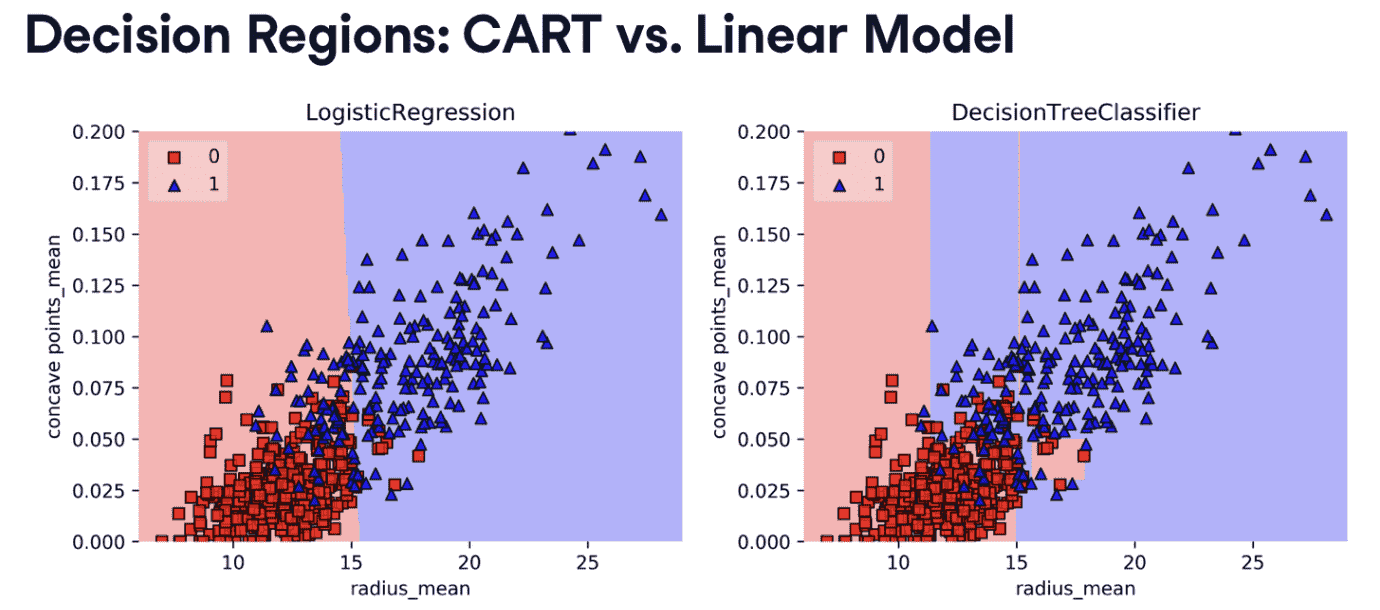
截屏2023-02-20 09.08.17

information gain（IG）

在某个内部节点上，decisionTree会问一个关于特征f和分裂点sp的问题，但是如何判定要分裂哪一个特征是根据最大化IG实现的 $I G(\underbrace{f}_{\text {feature }}, \underbrace{s p}_{\text {split-point }})=I(\text { parent })-\left(\frac{N_{\text {left }}}{N} I(\text { left })+\frac{N_{\text {right }}}{N} I(\text { right })\right)$

Criteria to measure the Impurity of a node $I(node)$ :

gini index,

entropy

nodes are grown recursively (DT除root外的任一节点必定依赖其祖先存在)
At each node, split the data based on:
- feature $f$ and split-point $s p$ to maximize $I G$ (node).
- If $I G( node )=0$, declare the node a leaf. （不受约束的DT）
- 到达max-depth强制终止（受约束的DT）

Decision Tree for Regression

分类问题是预测离散类别，回归问题是预测连续数值。

from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error as MSE

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=3)

# Instantiate a DecisionTreeRegressor 'dt'
dt = DecesionTreeRegressor(max_depth=4,min_samples_leaf=0.1,random_state=3)

dt.fit(X_train,y_train)
y_pred = dt.predict(X_test)

计算MSE
mse_dt = MSE(y_test,Y_pred)

# 计算RMSE
rmse_dt = mse_dt**(1/2)
print(rmse_dt)

Information Criterion for Regression-Tree

\[\begin{gathered} I(\text { node })=\underbrace{\mathrm{MSE}(\text { node })}_{\text {mean-squared-error }}=\frac{1}{N_{\text {node }}} \sum_{i \in \text { node }}\left(y^{(i)}-\hat{y}_{\text {node }}\right)^2 \\ \underbrace{\hat{y}_{\text {node }}}_{\text {mean-target-value }}=\frac{1}{N_{\text {node }}} \sum_{i \in \text { node }} y^{(i)} \end{gathered}\]

每次节点分裂的位置都是在均值附近，具体来说，是使得 $\min _{j, s}\left[\min _{c_1} \sum_{x_i \in R_1(j, s)}\left(y_i-c_1\right)^2+\min _{c_2} \sum_{x_2 \in R_2(j, s)}\left(y_i-c_2\right)^2\right]$ 最小，其中$c_1,c_2$分别是左右切分集合的均值

Linear regression & Regression tree

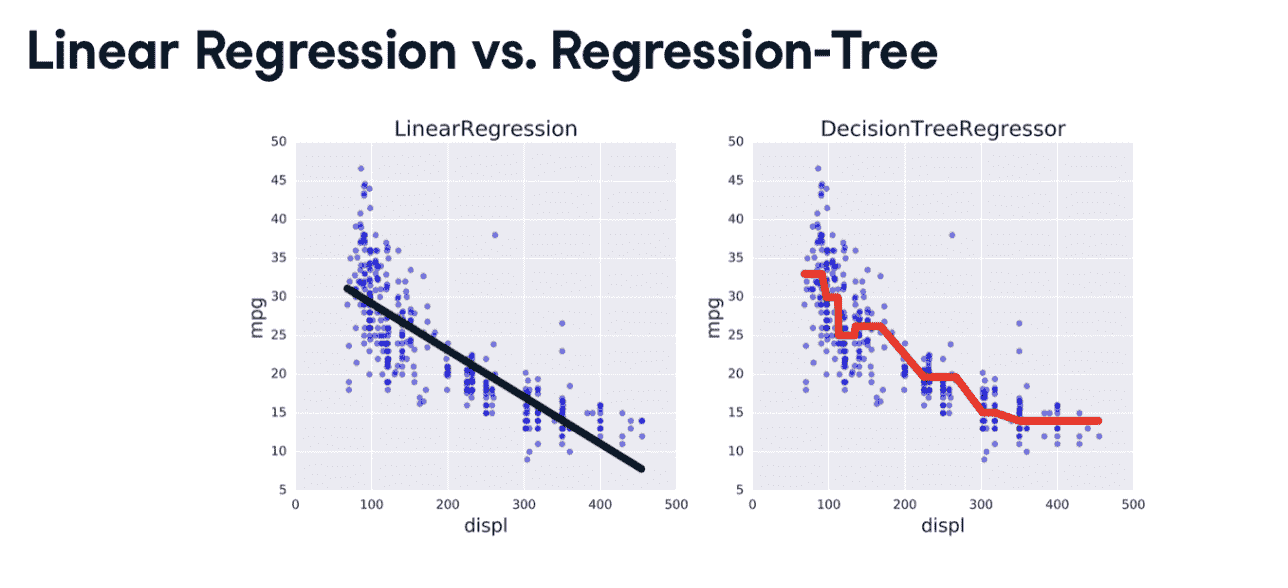
截屏2023-02-20 10.22.25

The bias-variance trade-off (ensembling)

偏差-方差权衡

supervised learning：

假设：存在未知函数$f$, $y=f(x)$

目标：Find a model $\hat{f}$ that best approximates $f: \hat{f} \approx f$ （$\hat{f}$ can be Logistic Regression, Decision Tree, Neural Network …）且$\hat{f}$在验证集上要有较低预测误差

注意：训练过程中要降低噪声的影响

Overfitting & Underfitting

Overfitting: $f(x)$ fits the training set noise.

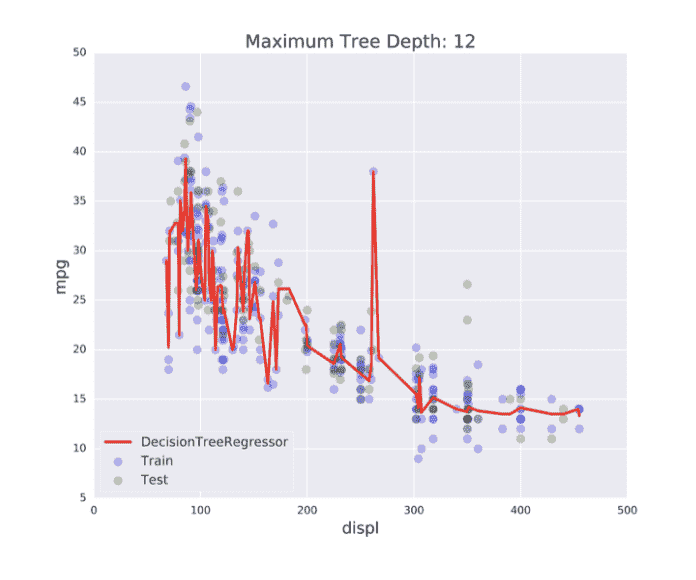
截屏2023-02-20 11.37.06

低训练集误差，高测试集误差

Underfitting: $\hat{f}$ is not flexible enough to approximate $f$.

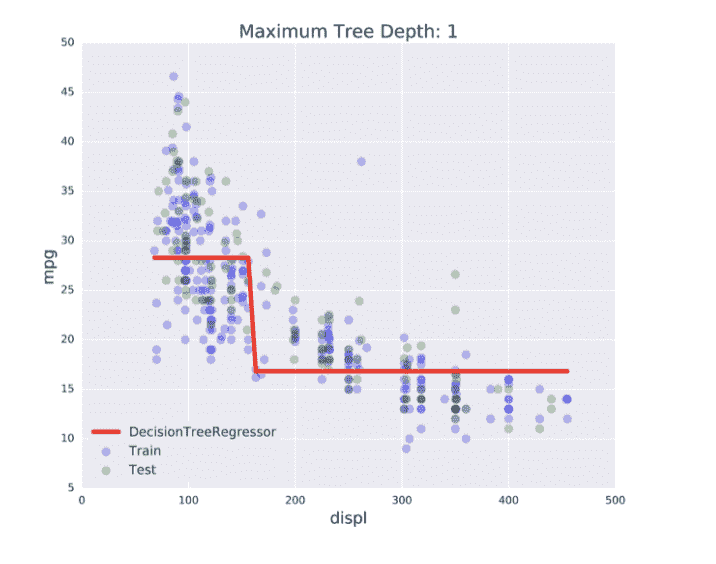
截屏2023-02-20 11.39.39

高训练集误差，高测试集误差（两者大致相等）

Generalization Error

泛化误差，只针对有监督模型。泛化误差是指模型在新数据上的表现与在训练数据上的表现之间的差异，是评估模型泛化能力的重要指标。

Generalization Error of $\hat{f}$ : Does $\hat{f}$ generalize well on unseen data?
It can be decomposed as follows: Generalization Error of $\hat{f}= bias ^2+ variance + irreducible\ error$
bias: on avarage, how much $\hat{f} \neq f$

高bias产生欠拟合

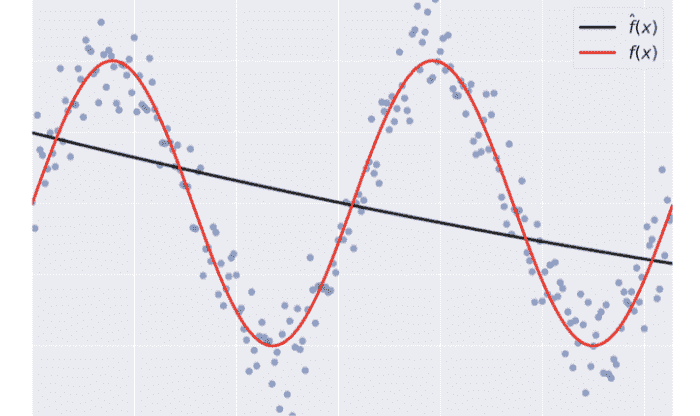
截屏2023-02-20 11.44.02

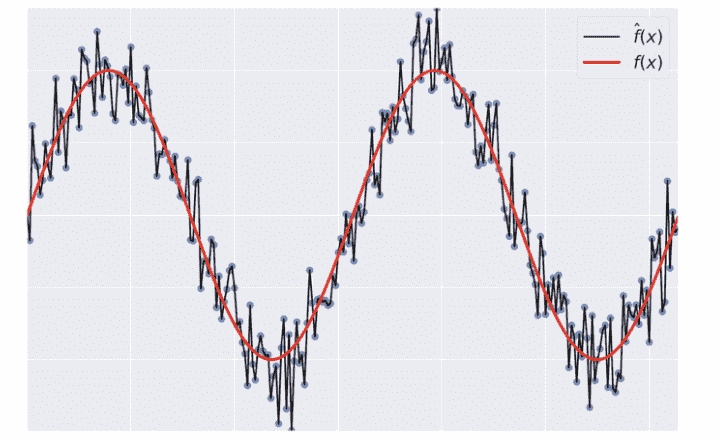
Variance: how much $\hat{f}$ is inconsistent over different training sets.

高方差模型产生过拟合

截屏2023-02-20 11.46.45

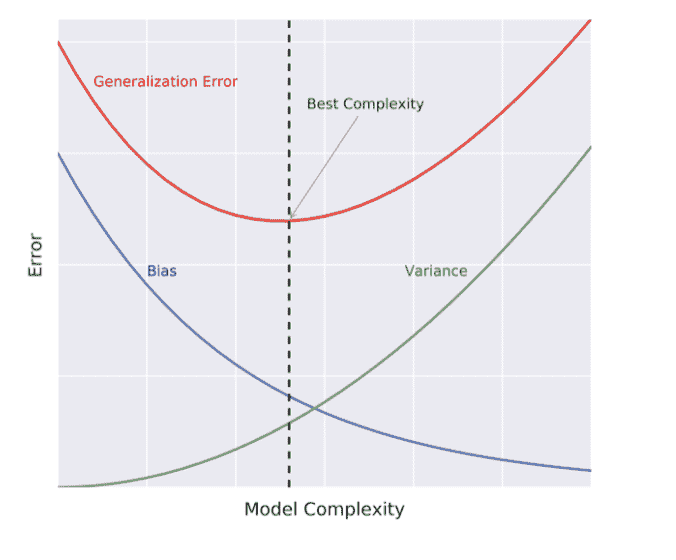
Model Complexity

模型复杂度决定模型拟合数据的灵活性

截屏2023-02-20 11.48.21

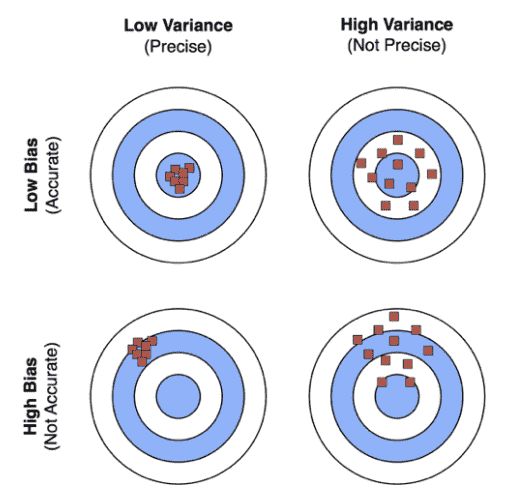
一个有趣的例子，假设$\hat{f}$是射中靶心

截屏2023-02-20 11.49.32

Cross-Validation (CV) 判定过 (欠) 拟合

K-Fold CV

Hold-Out CV

K-Fold CV

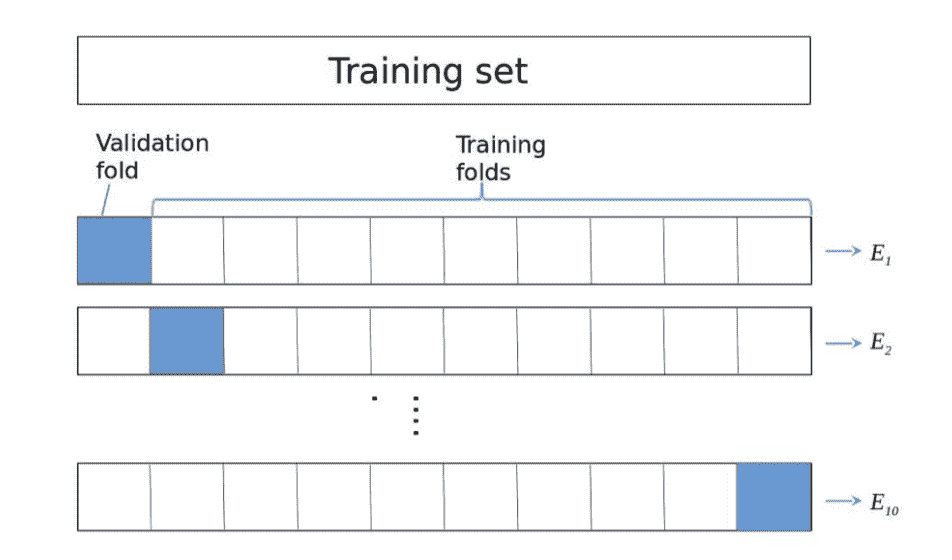
截屏2023-02-20 17.04.21

$\mathrm{CV}{error} $=$\frac{E_1+\ldots+E{10}}{10}$

每次在n-1折上训练，剩下最后一折测试；循环n次后计算误差平均值；

1）If $\hat{f}$ suffers from high variance: CV error of $\hat{f}>$ training set error of $\hat{f}$.

$\hat{f}$ is said to overfit the training set. To remedy overfitting:
- decrease model complexity, for ex: decrease max depth, increase min samples per leaf, …
- gather more data,..

2）If $\hat{f}$ suffers from high bias: CV error of $\hat{f} \approx$ training set error of $\hat{f}»$ desired error.

$\hat{f}$ is said to underfit the training set. To remedy underfitting:
- increase model complexity，for ex: increase max depth, decrease min samples per leaf, …
- gather more relevant features

from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error as MSE
from sklearn.model_selection import cross_val_score

# set seed for reproducibility
SEED = 123

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=SEED)

# Instantiate a DecisionTreeRegressor 'dt'
dt = DecesionTreeRegressor(max_depth=4,min_samples_leaf=0.14,random_state=SEED)

# n_jobs=-1调用所有cpu，得到的是长度为10的数组
MSE_CV = - cross_val_score(dt,X_train,y_train,cv=10,scoring='neg_mean_squared_error',njobs=-1) 

# 这表明cross_val_score不影响模型拟合
dt.fit(X_train,y_train)
y_pred_train = dt.predict(X_train)
y_pred_test = dt.predict(X_test)

# 计算CV_MSE
print('CV MSE: {:.2f}'.format(MSE_CV.mean()))

print('Train MSE: {:.2f}'.format(MSE(y_train,y_pred_train)))

print('Test MSE: {:.2f}'.format(MSE(y_test,y_pred_test)))
# Notice how the CV and test set errors are roughly equal.
# CV误差和测试集误差大致相等

Ensemble Learning

集成学习是一种监督学习

Train different models on the same dataset.
Meta-model: aggregates predictions of individual model.

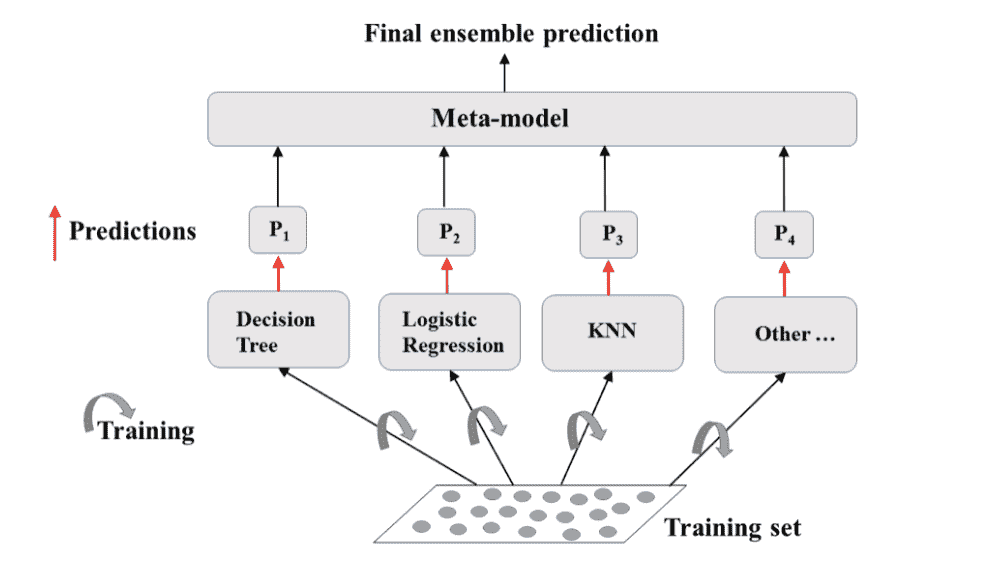
截屏2023-02-20 21.30.12

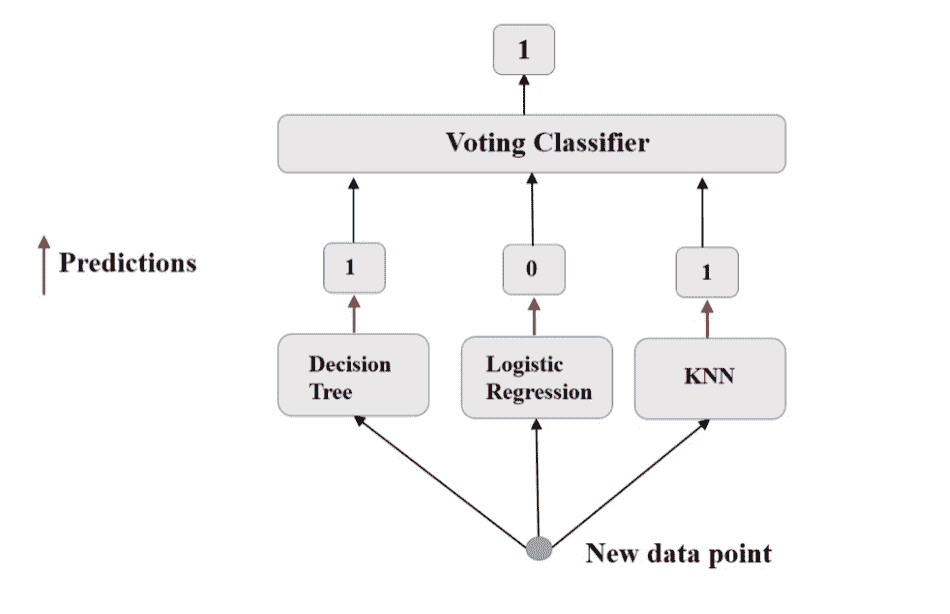
Voting Classifier

对于二分类任务，N个投票器给出N个预测，非0即1。

Hard vote

截屏2023-02-20 21.33.27

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split

from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifer
from sklearn.neighbors import KneighborsClassifier as KNN
from sklearn.ensemble import VotingClassifier

SEED = 1

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=SEED)

lr = LogisticRegression(random_state=SEED)
knn = KNN()
dt = DecisionTreeClassifier(random_state=SEED)

classifiers = [('Logistic Regression',lr),
('K Nearest Neighbours',knn),
('Classification tree',dt)]

for clf_name,clf in classifiers:
	clf.fit(X_train,y_train)
	y_pred=clf.predict(X_test)
	print('{:s}:{:.3f}'.format(clf_name,accuracy_score(y_test,y_pred)))
	
vc = VotingClasssifier(estimator=classifiers)

vc.fit(X_train,y_train)
y_pred = vc.predict(X_test)
print('{:s}:{:.3f}'.format("vc",accuracy_score(y_test,y_pred)))

Bagging (Bootstrap) and Random Forests

Bagging (Bootstrap) technic

Bagging: Bootstrap Aggregation

对比voting和Bagging

Voting 使用相同数据集，不同算法

Bagging 使用训练集的若干不同子集，相同算法

结论：Bagging 能够减小单独一个模型的方差（variance）

Bootstrap Technics

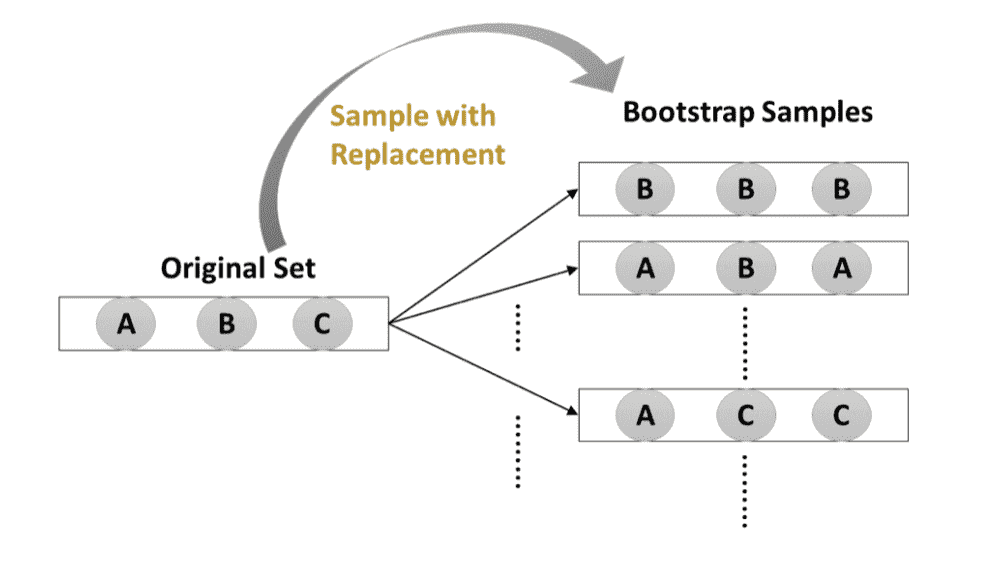
截屏2023-02-21 09.54.24

Bagging Training

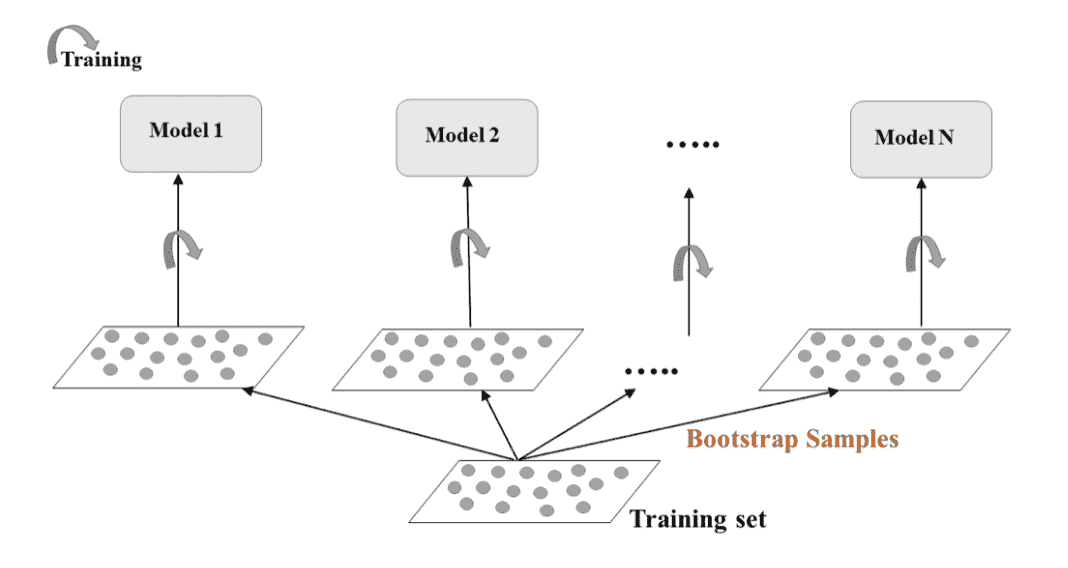
截屏2023-02-21 09.56.52

Bootstrap model

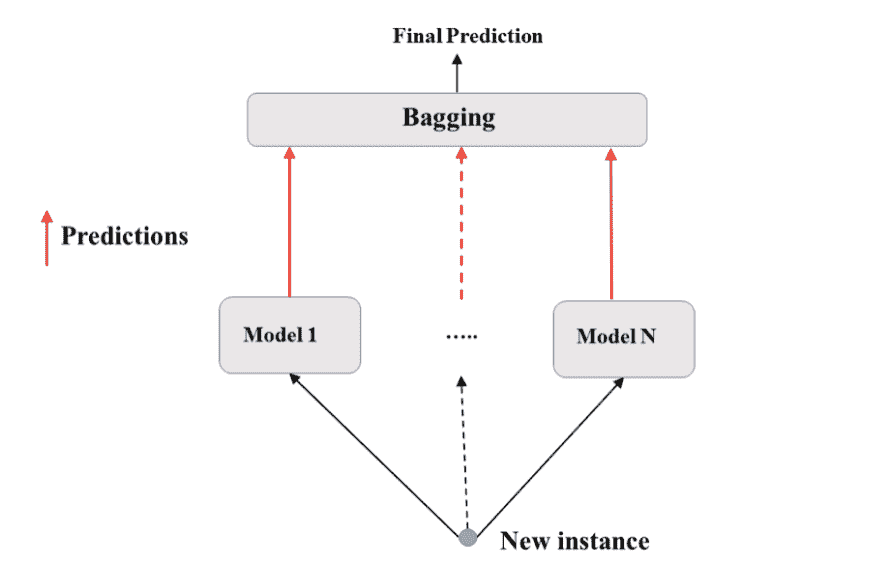
截屏2023-02-21 09.57.15

截屏2023-02-21 09.57.52

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier

SEED = 1

X_train, X_test, y_train, y_test = train_test_split(X,y,stratify=y,test_size=0.3,random_state=SEED)

dt = DecisionTreeClassifier(max_depth=4,min_samples_leaf=0.16,random_state=SEED)
	
bc = BaggingClasssifier(base_estimator=dt,n_estimators=300,n_jobs=-1)

bc.fit(X_train,y_train)
y_pred = bc.predict(X_test)
print('{:s}:{:.3f}'.format("vc",accuracy_score(y_test,y_pred)))

Out of Bag Evaluation

on average, for each model, 63% of the training instances are samples, the remaining 37% constitute the OOB instances.

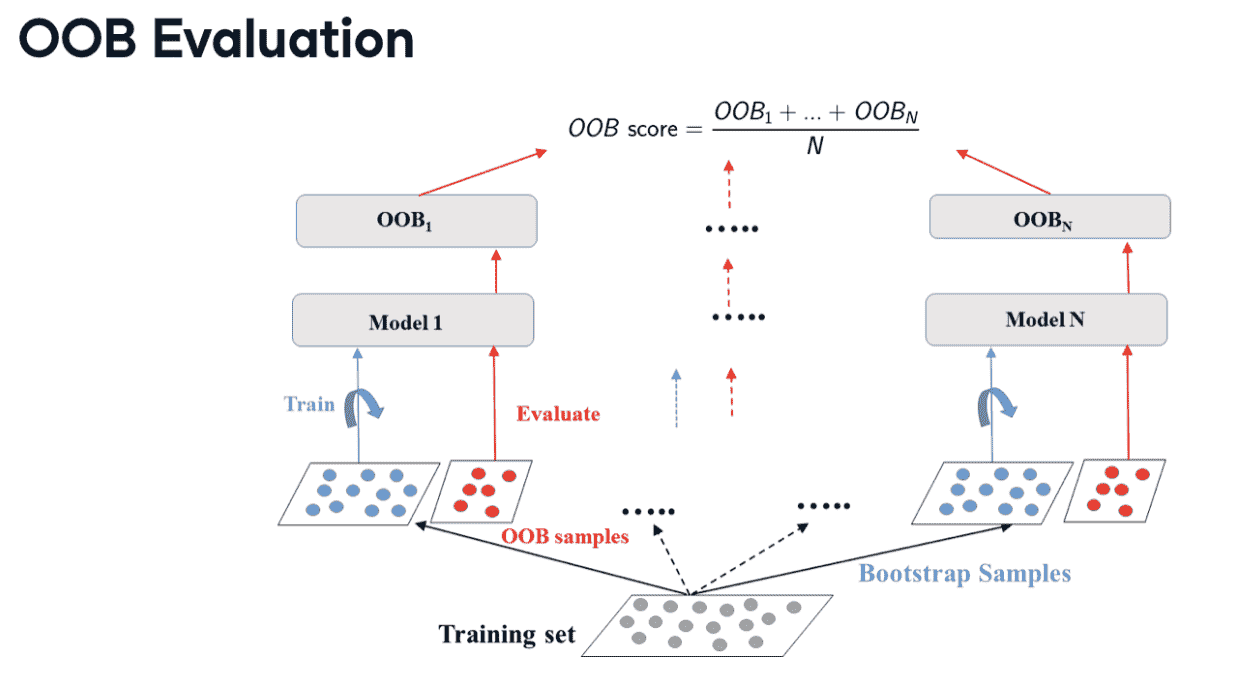
截屏2023-02-21 10.22.29

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier

SEED = 1

X_train, X_test, y_train, y_test = train_test_split(X,y,stratify=y,test_size=0.3,random_state=SEED)

dt = DecisionTreeClassifier(max_depth=4,min_samples_leaf=0.16,random_state=SEED)
	
# Note that in scikit-learn, the OOB-score corresponds to the accuracy for classifiers and the r-squared score for regressors
bc = BaggingClasssifier(base_estimator=dt,oob_score=True,n_estimators=300,n_jobs=-1)

bc.fit(X_train,y_train)
y_pred = bc.predict(X_test)
print('{:s}:{:.3f}'.format("test acc",accuracy_score(y_test,y_pred)))
print('{:s}:{:.3f}'.format("oob acc",bc.oob_score_))

Random Forest

相比Bagging (Bootstrap)，random的base_estimator使用所有数据预测，但是选取的是小于总特征数的随机d个子特征; scikit-learn中，d默认为总特征数的平方根。

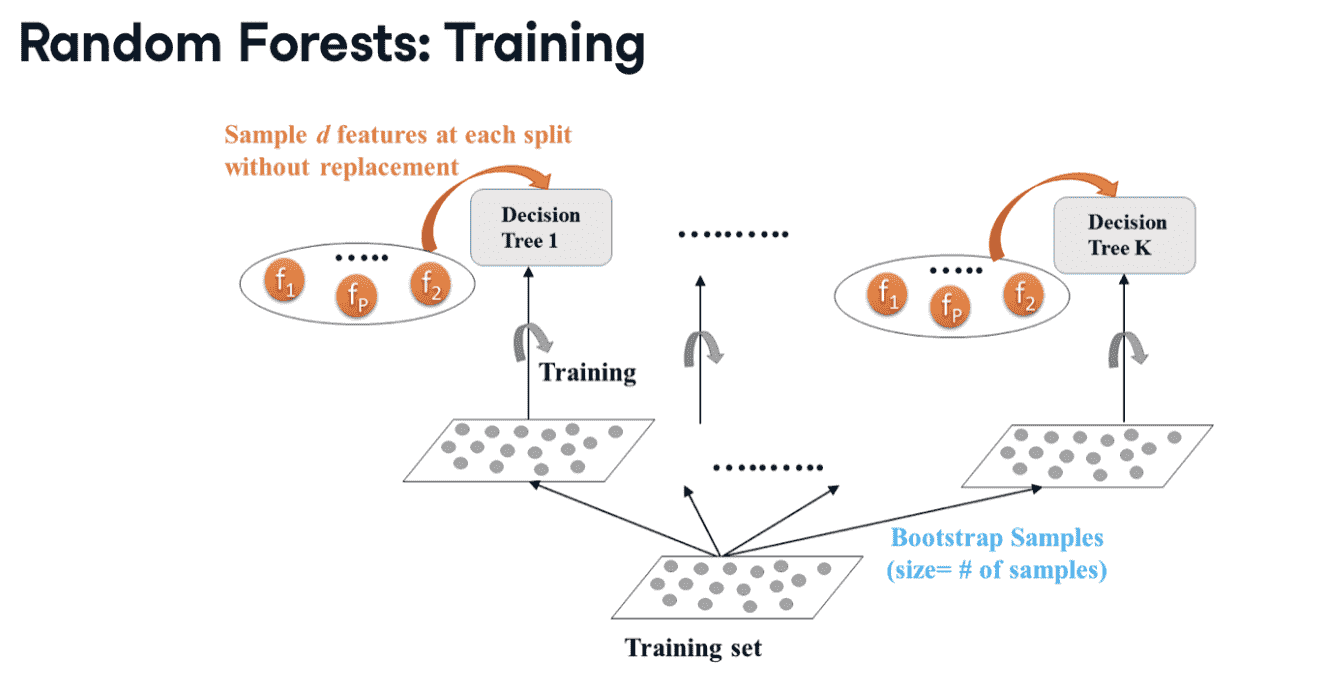
截屏2023-02-21 10.39.51

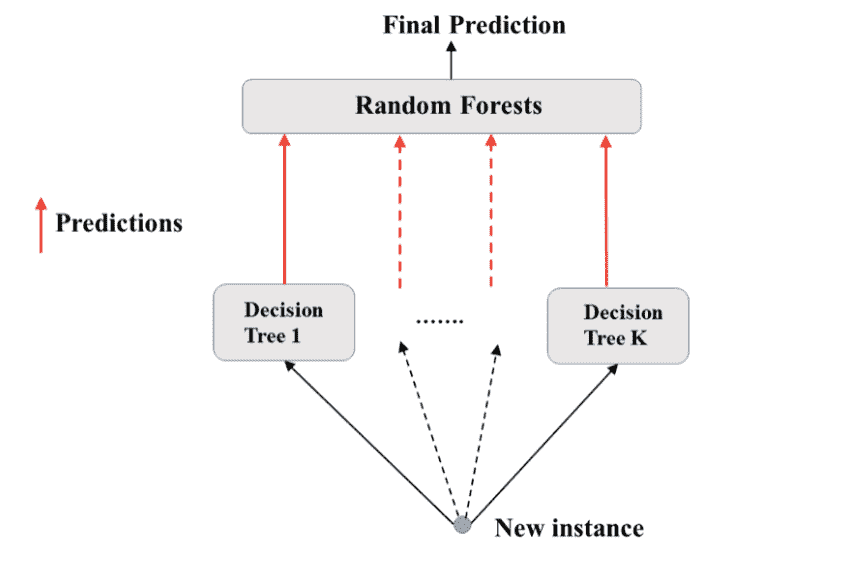
截屏2023-02-21 10.41.13

截屏2023-02-21 10.42.04

RF一般会比单个模型的Variance要低

from sklearn.metrics import mean_squared_error as MSE
from sklearn.model_selection import train_test_split

from sklearn.tree import RandomForestRegressor

SEED = 1

X_train, X_test, y_train, y_test = train_test_split(X,y,stratify=y,test_size=0.3,random_state=SEED)

rf = RandomForestRegressor(n_estimators=400,min_samples_leaf=0.12,random_state=SEED)

rf.fit(X_train,y_train)
y_pred = rf.predict(X_test)
rmse_test = MSE(y_test,y_pred)**(1/2)

Feature Importance

Tree-based methods: enable measuring the importance of each feature in prediction.

In sklearn:

How much the tree nodes use a particular feature (weighted avarage) to reduce impurity
Accessed using the attribute feature_importance_
请注意，特征的重要性以百分比表示，表示该特征在训练和预测中的权重。

import pandas as pd
import matplotlib.pyplot as plt

importances_rf = pd.Series(rf.feature_importances_, index=X.columns)

sorted_importances_rf = importances_rf.sort_values()

sorted_importances_rf.plot(kind='barh',color='lightgreen'); plt.show()

Boosting (AdaBoost and Gradient Boosting)

Boosting

Boosting: ensemble method combing several weak learners to form a strong learner.
Weak learner: model doing slightly better than random guessing. eg. Decision stump (CART with max_depth=1)
多个weak learner顺序训练，后继尝试纠正前任错误。

Adaboost （Ada代表自适应）

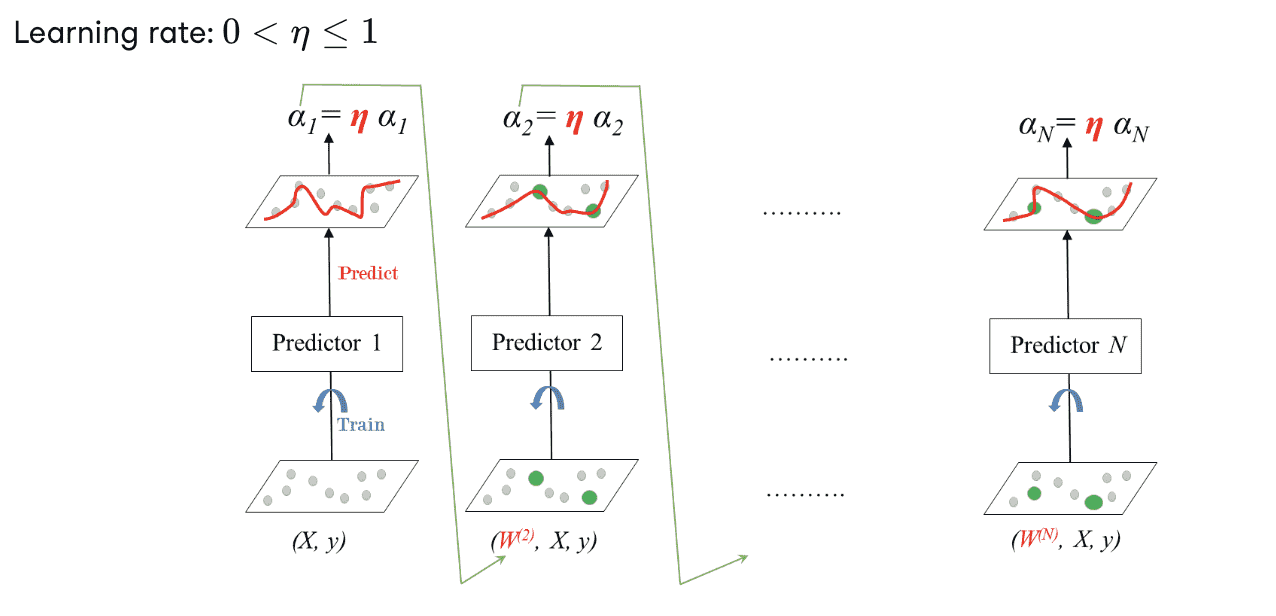
截屏2023-02-22 11.24.44

逐步关注预测错误的instance，学习率逐步缩减。较小的 $\eta$ 需要由较多的顺序分类器补偿

截屏2023-02-22 11.28.16

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import train_test_split

SEED = 1

X_train, X_test, y_train, y_test = train_test_split(X,y,stratify=y,test_size=0.3,random_state=SEED)

dt = DecisionTreeClassifier(max_depth=1,random_state=SEED)

adb_clf = AdaBoostClassifier(base_estimator=dt,n_estimaor=100)

adb_clf.fit(X_train,y_train)
y_pred_proba = rf.predict_proba(X_test)[:,1]  // 第一列是负例的概率，第二列是正例的概率
adb_clf_roc_auc_score = roc_auc_score(y_test,y_pred_proba)

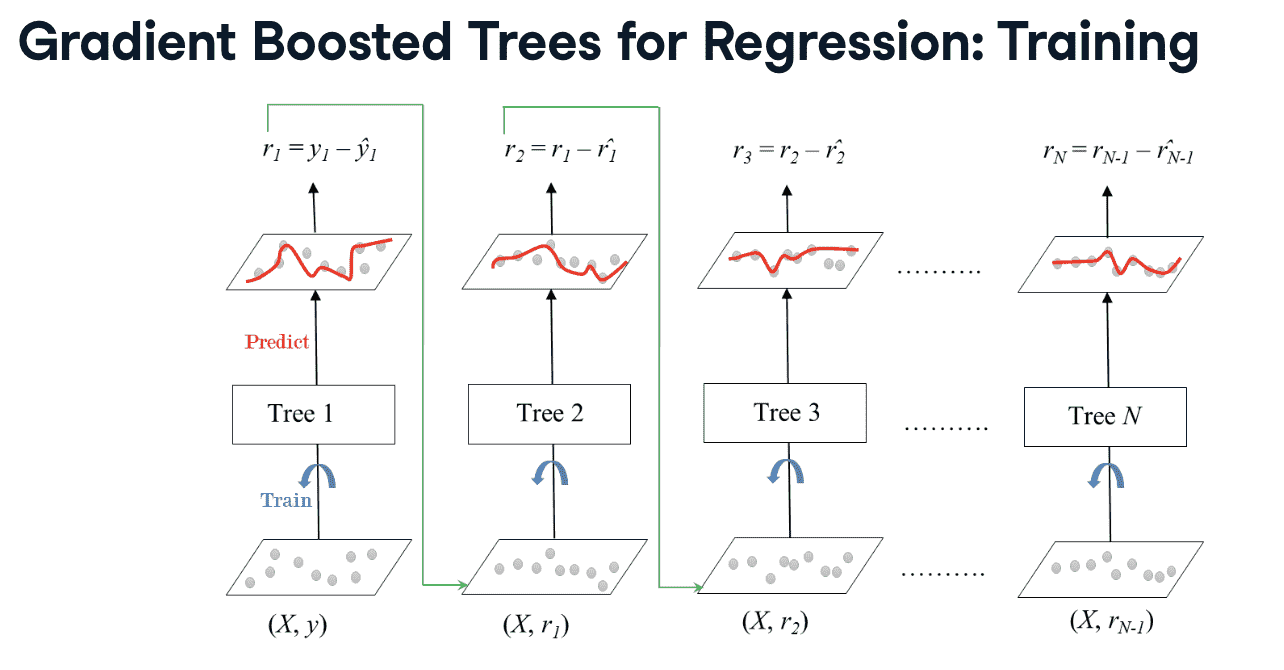
Gradient Boosting (GB)

Gradient Boosted Trees

后继在前训练器下训练，与adaboost不同，后继用的label是前继的残差

截屏2023-02-24 15.42.13

Shrinkage

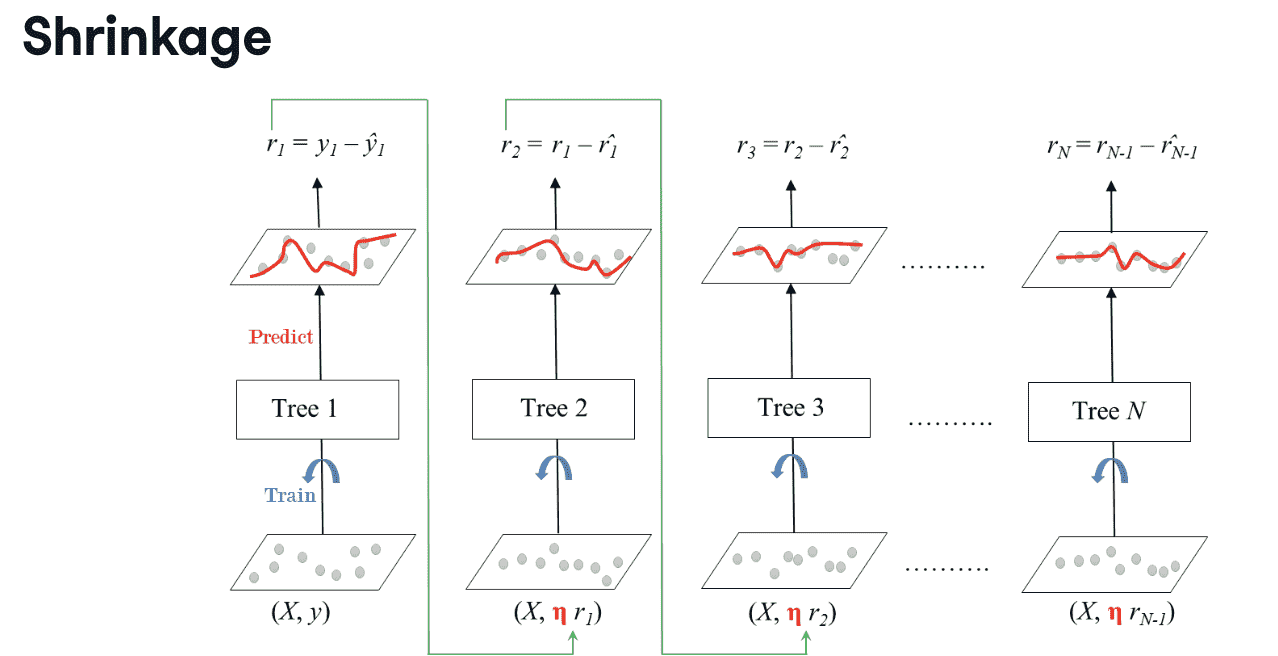
截屏2023-02-24 15.45.15

Decreasing the learning rate $\eta$ needs to be compensated by increasing the number of estimators in order for the ensemble to reach a certain performance.

截屏2023-02-24 15.48.15

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error as MSE
from sklearn.model_selection import train_test_split

SEED = 1

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=SEED)

gbt = GradientBoostingRegressor(n_estimators=300,max_depth=1,random_state=SEED)

gbt.fit(X_train,y_train)
y_pred = gbt.predict(X_test)
rmse_test = MSE(y_test,y_pred)**(1/2)

Stochastic Gradient Boosting (SGB)

cons of GBT：不同分类器可能会使用相同特征、相同分割点

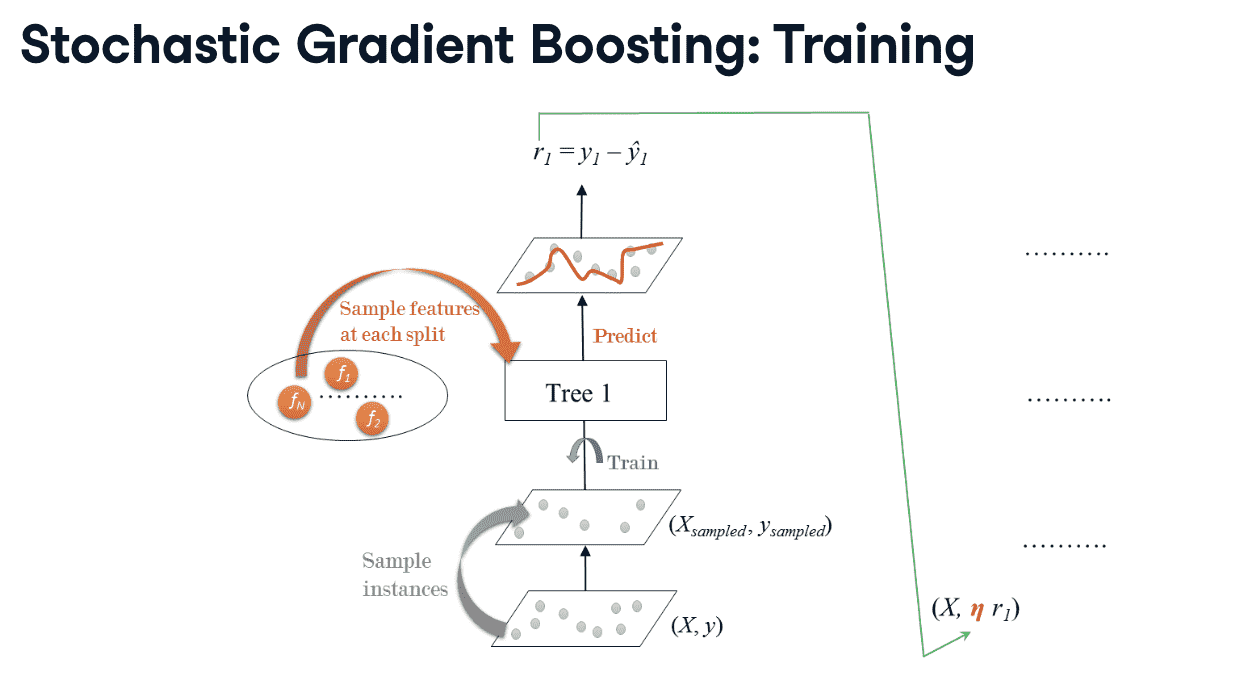
截屏2023-02-24 16.03.41

改进：
- 每棵树都在training_set的某些列子集上训练
- 训练实例（40%-80% of training set）在训练集上不重复采样（sampled without replacement）
- 在选分裂点是，选取的特征也是不重复采样

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error as MSE
from sklearn.model_selection import train_test_split

SEED = 1

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=SEED)

sgbt = GradientBoostingRegressor(subsample=0.8,max_features=0.2,n_estimators=300,max_depth=1,random_state=SEED)

sgbt.fit(X_train,y_train)
y_pred = sgbt.predict(X_test)
rmse_test = MSE(y_test,y_pred)**(1/2)

Model Tuning

To obtain a better performance, the hyperparameters of a machine learning should be tuned.

截屏2023-02-24 16.14.56

截屏2023-02-24 16.16.38

methods of hyperparameter tuning

Grid Search
Random Search
Bayesian Optimization
Genetic Algorithm

Grid Search

截屏2023-02-24 16.31.51

截屏2023-02-24 20.12.58

输出参数

from sklearn.tree import DecisionTreeClassifier

SEED = 1

dt = DecisionTreeClassifier(random_state=SEED)

print(dt.get_params())

example

from sklearn.model_selection import GridSearchCV

params_dt = {
	'max_depth':[3,4,5,6],
	'min_samples_leaf':[0.04,0.06,0.08],
	'max_features':[0.2,0.4,0.6,0.8]
}

grid_dt = GridSearchCV(estimator=dt,param_grid=params_dt,
scoring='accuracy',cv=10,n_jobs=-1)

grid_dt.fit(X_train,y_train)

best_hyperparams = grid_dt.best_params_
print(best_hyperparams)
best_cv_score = grid_dt.best_score_
print(best_cv_scoree)
best_model = grid_dt.best_estimator_
// Note that this model is fitted on the whole training set because the refit parameter of GridSearchCV is set to True by default
test_acc = best_model.score(X_test,y_test)

Tuning on RF’s Hyperparameters

from sklearn.metrics import mean_squared_error as MSE
from sklearn.model_selection import train_test_split

from sklearn.tree import RandomForestRegressor

SEED = 1

rf = RandomForestRegressor(random_state=SEED)

pf.get_params()

from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error as MSE

params_rf = {
'n_estimators':[300,400,500],
'max_depth':[4,6,8],
'min_samples_leaf':[0.1,0.2],
'max_features':['log2','sqrt']
}

grid_rf = GridSearchCV(estimator=rf,param_grid=params_rf,cv=3,scoring='neg_mean_squared_error',verbose=1,n_jobs=-1)
// Note that the parameter verbose controls verbosity

grid_rf.fit(X_train,y_train)

best_hyperparams = grid_rf.best_params_

best_model = grid_rf.best_estimator_

y_pred = best_model.predict(X_test)
rmse_test=MSE(y_test,y_pred)**(1/2)

verbose=0 表示不输出任何日志信息。

verbose=1 表示输出进度条信息。

verbose=2 表示输出每次交叉验证的结果。

Tree-based Model入门&应用

ML&DL中的Tree-based model综述