[TOC]
A Cheatshit for SLAM
SLAM简介
SLAM是Simultaneous Localization and Mapping的缩写,中文译作“同时定位与地图构建”山。它是指搭载特定传感器的主体,在没有环境先验信息的情况下,于运动过程中建立环境的模型,同时估计自己的运动。如果这里的传感器主要为相机,那就称为“视觉SLAM”。
SLAM结构
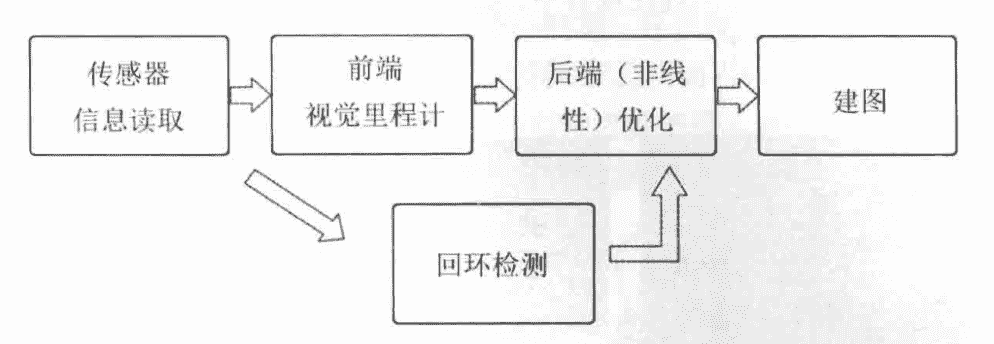
- 传感器信息读取。在视觉SLAM中主要为相机图像信息的读取和预处理。如果是在机器人中,还可能有码盘、惯性传感器等信息的读取和同步。
- 前端视觉里程计(Visual Odometry,VO)。视觉里程计的任务是估算相邻图像间相机的运动,以及局部地图的样子。VO又称为前端(Front End) 。
- 后端(非线性)优化(Optimization)。后端接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对它们进行优化,得到全局一致的轨迹和地图。由于接在VO之后, 又称为后端(Back End)
- 回环检测(Loop Closure Detection)。回环检测判断机器人是否到达过先前的位置。如果检测到回环,它会把信息提供给后端进行处理。
- 建图(Mapping)。它根据估计的轨迹,建立与任务要求对应的地图。
Visual Odometry
估计两个图像之间的位移,但是不可避免出现累计漂移(accumulating drift),因此需要Optimization(解决噪声)和Loop Closure Detection(检测“回到原点这件事”)
- 前端,CV中的特征提取、匹配
Optimization
从带噪声的数据中估计整个系统的状态,已经状态估计的不确定性(最大后验概率估计,Maximum-a-Posteriori, MAP)
- 后端,滤波、非线性优化算法
Loop Closure Detection
计算图像间的相似性,判断是否到达过同一个地方,告诉后端优化
Mapping
主要看需求,事实上有很多种地图。
- 度量地图,Metric Map
- 稀疏(Sparse):只管路标(Landmark),其他可以忽略
- 稠密(Dense):分为稠密的Grid(二维地图)、Voxel(三维地图),这些格子有三种状态(占据、空闲、未知)
- 拓扑地图,Topological Map
拓扑地图是一个Graph,更多考虑的是连通性
SLAM的数学描述
\[\left\{\begin{array}{ll} \boldsymbol{x}_k=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_k, \boldsymbol{w}_k\right), & k=1, \cdots, K \\ \boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_j, \boldsymbol{x}_k, \boldsymbol{v}_{k, j}\right), & (k, j) \in \mathcal{O} \end{array} .\right.\]第一个方程是运动方程,第二个是观测方程.
$k$是传感器采样的时刻
$x_k$ 是$k$ 时刻机器人所在位置,$u_k$ 是$k$ 时刻传感器读数,$w_k、v_{k,j}$ 分别是两个估计的噪声
$z_{k,j}$ 是$k$ 时刻看到路标点$y_j$产生的观测数据(建图数据),$y_j$ 是$j$ 路标点数据
$O$ 是集合,记录在哪个时刻观测哪个路标
状态估计问题的求解按运动观测方程是否为线性、噪声是否服从高斯分布分为:
- 线性高斯系统(Linear Gaussian):MAP可以由Kalman Filter给出
- 非线性非高斯系统:需要Extended Kalman Filter+非线性优化+Particle Filter+Graph Optimization
三维空间下的刚体运动
基础知识
- 内积
- 外积
其中,$\boldsymbol{a}^{\wedge}$ 是 $\boldsymbol{a}$ 的反对称矩阵(Skew-symmetric Matrix)
- 坐标系旋转
利用向量在各个坐标系下的不变性,可以得到旋转矩阵(Direction Cosine Matrix,因为本质上是各基向量夹角Cosine): \(\left[\begin{array}{l} a_1 \\ a_2 \\ a_3 \end{array}\right]=\left[\begin{array}{lll} \boldsymbol{e}_1^{\mathrm{T}} \boldsymbol{e}_1^{\prime} & \boldsymbol{e}_1^{\mathrm{T}} \boldsymbol{e}_2^{\prime} & \boldsymbol{e}_1^{\mathrm{T}} \boldsymbol{e}_3^{\prime} \\ \boldsymbol{e}_2^{\mathrm{T}} \boldsymbol{e}_1^{\prime} & \boldsymbol{e}_2^{\mathrm{T}} \boldsymbol{e}_2^{\prime} & \boldsymbol{e}_2^{\mathrm{T}} \boldsymbol{e}_3^{\prime} \\ \boldsymbol{e}_3^{\mathrm{T}} e_1^{\prime} & \boldsymbol{e}_3^{\mathrm{T}} \boldsymbol{e}_2^{\prime} & \boldsymbol{e}_3^{\mathrm{T}} \boldsymbol{e}_3^{\prime} \end{array}\right]\left[\begin{array}{c} a_1^{\prime} \\ a_2^{\prime} \\ a_3^{\prime} \end{array}\right] \stackrel{\text { def }}{=} \boldsymbol{R} \boldsymbol{a}^{\prime}\) 这意味着,$\boldsymbol{R}^{-1} $ 代表相反的旋转变换
n 维旋转矩阵 <=> n维度行列式为1的正交矩阵:
\[\mathrm{SO}(n)=\left\{\boldsymbol{R} \in \mathbb{R}^{n \times n} \mid \boldsymbol{R} \boldsymbol{R}^{\mathrm{T}}=\boldsymbol{I}, \operatorname{det}(\boldsymbol{R})=1\right\}\]$\mathrm{SO}(n)$ 是特殊正价群,代表n维空间的旋转
- 坐标系欧式变换(旋转+平移)
旋转$R_{12}$是指“把坐标系2的向量变换到坐标系1”中。
平移$t_{12}$,它实际对应的是坐标系1原点指向坐标系2原点的向量,在坐标系1下取的坐标。
- 齐次坐标变换
\[\left[\begin{array}{l} \boldsymbol{a}^{\prime} \\ 1 \end{array}\right]=\left[\begin{array}{ll} \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right]\left[\begin{array}{l} \boldsymbol{a} \\ 1 \end{array}\right] \stackrel{\text { def }}{=} \boldsymbol{T}\left[\begin{array}{l} \boldsymbol{a} \\ 1 \end{array}\right] .\]欧式坐标变换的常数项合并到矩乘中,$\boldsymbol{T}$是变换矩阵
因此得到任意3维欧式变化的特殊欧式群(Special Euclidean Group): \(\mathrm{SE}(3)=\left\{\boldsymbol{T}=\left[\begin{array}{ll} \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right] \in \mathbb{R}^{4 \times 4} \mid \boldsymbol{R} \in \mathrm{SO}(3), \boldsymbol{t} \in \mathbb{R}^3\right\}\) 反向变换为: \(\boldsymbol{T}^{-1}=\left[\begin{array}{cc} \boldsymbol{R}^{\mathrm{T}} & -\boldsymbol{R}^{\mathrm{T}} \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right]\)
旋转向量&欧拉角
- 旋转向量
旋转向量(或轴角/角轴,Axis-Angle):使用一个向量,其方向与旋转轴一致,而长度等于旋转角。
使用一个旋转向量和一个平移向量即可表达一次变换。维数正好是六维。
旋转向量到旋转矩阵的表示,Rodrigues’s Formula: \(\boldsymbol{R}=\cos \theta \boldsymbol{I}+(1-\cos \theta) \boldsymbol{n} \boldsymbol{n}^{\mathrm{T}}+\sin \theta \boldsymbol{n}^{\wedge}\) 其中,$\theta$ 是旋转度数,$n$是旋转轴,$\theta n$为旋转向量。
逆变换: \(\begin{aligned} \operatorname{tr}(\boldsymbol{R}) & =\cos \theta \operatorname{tr}(\boldsymbol{I})+(1-\cos \theta) \operatorname{tr}\left(\boldsymbol{n} \boldsymbol{n}^{\mathrm{T}}\right)+\sin \theta \operatorname{tr}\left(\boldsymbol{n}^{\wedge}\right) \\ & =3 \cos \theta+(1-\cos \theta) \\ & =1+2 \cos \theta \end{aligned}\) 因此: \(\theta=\arccos \frac{\operatorname{tr}(\boldsymbol{R})-1}{2} .\)
- 欧拉角
欧拉角$[r,p,y]^T$定义为绕三个坐标轴的旋转角,ZYX角这样定义:
1.绕物体的Z轴旋转,得到偏航角yaw。 2.绕旋转之后的Y轴旋转,得到俯仰角pitch。 3.绕旋转之后的X轴旋转,得到滚转角roll。
但是欧拉角会产生万向锁问题(Gimbal Lock):在俯仰角为土90°时, 第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由3次旋转变成了2次旋转)。这被称为奇异性问题,表现在所有用三个实数表达$SO(3)$的问题上。
四元数
一个四元数 $\boldsymbol{q}$ 拥有一个实部和三个虚部。也可以用一个标量和一个向量来表达四元数。本质上就是旋转向量,即虚部为旋转轴,实部为旋转角度。 \(\boldsymbol{q}=q_0+q_1 \mathrm{i}+\mathrm{q}_2 \mathrm{j}+\mathrm{q}_3 \mathrm{k}=[s, \boldsymbol{v}]^{\mathrm{T}}, \quad s=q_0 \in \mathbb{R}, \quad \boldsymbol{v}=\left[q_1, q_2, q_3\right]^{\mathrm{T}} \in \mathbb{R}^3 .\) $s$ 称为四元数的实部, 而 $\boldsymbol{v}$ 称为它的虚部。如果一个四元数的虚部为 $\mathbf{0}$, 则称为实四元数; 反之, 若它的实部为 0 , 则称为虚四元数。其中, $i, j, k$ 为四元数的三个虚部。这三个虚部满足以下关系式: \(\left\{\begin{array}{l} \mathrm{i}^2=\mathrm{j}^2=\mathrm{k}^2=-1 \\ \mathrm{ij}=\mathrm{k}, \mathrm{ji}=-\mathrm{k} \\ \mathrm{jk}=\mathrm{i}, \mathrm{kj}=-\mathrm{i} \\ \mathrm{ki}=\mathrm{j}, \mathrm{ik}=-\mathrm{j} \end{array}\right.\)
四元数运算
现有两个四元数 $\boldsymbol{q}_a, \boldsymbol{q}_b$: \(\boldsymbol{q}_a=s_a+x_a \mathrm{i}+\mathrm{y}_{\mathrm{a}} \mathrm{j}+\mathrm{z}_{\mathrm{a}} \mathrm{k}=\left[s_a, \boldsymbol{v}_a\right]^{\mathrm{T}}, \quad \mathrm{q}_{\mathrm{b}}=\mathrm{s}_{\mathrm{b}}+\mathrm{x}_{\mathrm{b}} \mathrm{i}+\mathrm{y}_{\mathrm{b}} \mathrm{j}+\mathrm{z}_{\mathrm{b}} \mathrm{k}=\left[s_b, \boldsymbol{v}_b\right]^{\mathrm{T}}\)
- 加减法
\(\boldsymbol{q}_a \pm \boldsymbol{q}_b=\left[s_a \pm s_b, \boldsymbol{v}_a \pm \boldsymbol{v}_b\right]^{\mathrm{T}}\)
- 乘法
乘法是把 $\boldsymbol{q}_a$ 的每一项与 $\boldsymbol{q}_b$ 的每项相乘, 最后相加, 虚部要按照式 (3.21) 进行。整理可得
\(\begin{aligned} \boldsymbol{q}_a \boldsymbol{q}_b= & s_a s_b-x_a x_b-y_a y_b-z_a z_b \\ & +\left(s_a x_b+x_a s_b+y_a z_b-z_a y_b\right) \mathrm{i} \\ & +\left(s_a y_b-x_a z_b+y_a s_b+z_a x_b\right) \mathrm{j} \\ & +\left(s_a z_b+x_a y_b-y_a x_b+z_a s_b\right) \mathrm{k} \end{aligned}\) 虽然稍为复杂, 但形式上是整齐有序的。如果写成向量形式并利用内外积运算, 该表达 会更加简洁: \(\boldsymbol{q}_a \boldsymbol{q}_b=\left[s_a s_b-\boldsymbol{v}_a^{\mathrm{T}} \boldsymbol{v}_b, s_a \boldsymbol{v}_b+s_b \boldsymbol{v}_a+\boldsymbol{v}_a \times \boldsymbol{v}_b\right]^{\mathrm{T}}\)
- 模长
四元数的模长定义为 \(\left\|\boldsymbol{q}_a\right\|=\sqrt{s_a^2+x_a^2+y_a^2+z_a^2}\) 两个四元数乘积的模即模的乘积。结论:单位四元数相乘后仍是单位四元数。 \(\left\|\boldsymbol{q}_a \boldsymbol{q}_b\right\|=\left\|\boldsymbol{q}_a\right\|\left\|\boldsymbol{q}_b\right\|\)
- 共轭
四元数的共轭是把虚部取成相反数: \(\boldsymbol{q}_a^*=s_a-x_a \mathrm{i}-\mathrm{y}_{\mathrm{a}} \mathrm{j}-\mathrm{z}_{\mathrm{a}} \mathrm{k}=\left[\mathrm{s}_{\mathrm{a}},-\mathrm{v}_{\mathrm{a}}\right]^{\mathrm{T}}\) 四元数共轭与其本身相乘, 会得到一个实四元数, 其实部为模长的平方: \(\boldsymbol{q}^* \boldsymbol{q}=\boldsymbol{q} \boldsymbol{q}^*=\left[s_a^2+\boldsymbol{v}^{\mathrm{T}} \boldsymbol{v}, \mathbf{0}\right]^{\mathrm{T}}\)
- 逆
一个四元数的逆为 \(\boldsymbol{q}^{-1}=\boldsymbol{q}^* /\|\boldsymbol{q}\|^2\) 按此定义, 四元数和自己的逆的乘积为实四元数 $\mathbf{1}:$ \(\boldsymbol{q} \boldsymbol{q}^{-1}=q^{-1} \boldsymbol{q}=1\) 如果 $\boldsymbol{q}$ 为单位四元数, 其逆和共轭就是同一个量。同时, 乘积的逆具有和矩阵相似的性质: \(\left(\boldsymbol{q}_a \boldsymbol{q}_b\right)^{-1}=\boldsymbol{q}_b^{-1} \boldsymbol{q}_a^{-1}\)
- 数乘
和向量相似, 四元数可以与数相乘: \(\mathrm{k} \boldsymbol{q}=[\mathrm{k} s, \mathrm{k} \boldsymbol{v}]^{\mathrm{T}}\)
四元数旋转
我们可以用四元数表达对一个点的旋转。假设有一个空间三维点 $\boldsymbol{p}=[x, y, z] \in \mathbb{R}^3$, 以及 一个由单位四元数 $\boldsymbol{q}$ 指定的旋转。三维点 $\boldsymbol{p}$ 经过旋转之后变为 $\boldsymbol{p}^{\prime}$ 。如果使用矩阵描述, 那么有 $\boldsymbol{p}^{\prime}=\boldsymbol{R} \boldsymbol{p}$ 。而如果用四元数描述旋转, 它们的关系又如何表达呢? 首先, 把三维空间点用一个虚四元数来描述: \(\boldsymbol{p}=[0, x, y, z]^{\mathrm{T}}=[0, \boldsymbol{v}]^{\mathrm{T}}\) 相当于把四元数的 3 个虚部与空间中的 3 个轴相对应。那么, 旋转后的点 $\boldsymbol{p}^{\prime}$ 可表示为这样的乘积: \(\boldsymbol{p}^{\prime}=\boldsymbol{q} \boldsymbol{p} \boldsymbol{q}^{-1}\) 这里的乘法均为四元数乘法, 结果也是四元数。最后把 $\boldsymbol{p}^{\prime}$ 的虚部取出, 即得旋转之后点的坐标。 并且, 计算结果的实部为 0 , 故为纯虚四元数。
相似、仿射、摄影变换
- 相似变换 相似变换比欧氏变换多了一个自由度, 它允许物体进行均匀缩放, 其矩阵表示为 \(\boldsymbol{T}_S=\left[\begin{array}{cc} s \boldsymbol{R} & \boldsymbol{t} \\ 0^{\mathrm{T}} & 1 \end{array}\right]\) 注意, 旋转部分多了一个缩放因子 $s$, 表示我们在对向量旋转之后, 可以在 $x, y, z$ 三个坐 标上进行均匀缩放。由于含有缩放, 相似变换不再保持图形的面积不变。你可以想象一 个边长为 1 的立方体通过相似变换后, 变成边长为 10 的样子 (但仍然是立方体)。三维相似变换的集合也叫作相似变换群, 记作 $\operatorname{Sim}(3)$ 。
- 仿射变换 仿射变换的矩阵形式如下: \(\boldsymbol{T}_A=\left[\begin{array}{ll} A & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right]\) 与欧氏变换不同的是, 仿射变换只要求 $\boldsymbol{A}$ 是一个可逆矩阵, 而不必是正交矩阵。仿射变换也叫正交投影。经过仿射变换之后, 立方体就不再是方的了, 但是各个面仍然是平行四边形。
- 射影变换 射影变换是最一般的变换, 它的矩阵形式为 \(\boldsymbol{T}_P=\left[\begin{array}{ll} \boldsymbol{A} & \boldsymbol{t} \\ \boldsymbol{a}^{\mathrm{T}} & v \end{array}\right] .\) 它的左上角为可逆矩阵 $\boldsymbol{A}$, 右上角为平移 $\boldsymbol{t}$, 左下角为缩放 $\boldsymbol{a}^{\mathrm{T}}$ 。由于采用了齐次坐标, 当 $v \neq 0$ 时, 我们可以对整个矩阵除以 $v$ 得到一个右下角为 1 的矩阵; 否则得到右下角为 0 的矩阵。因此, 2D 的射影变换一共有 8 个自由度, 3D 则共有 15 个自由度。射影变换是 现在讲过的变换中, 形式最为一般的。从真实世界到相机照片的变换可以看成一个射影变换。一个原本方形的地板砖, 在照片中是不是方形、也不是平行四边形。 \(\begin{array}{c|c|c|c} \hline \text { 变换名称 } & \text { 矩阵形式 } & \text { 自由度 } & \text { 不变性质 } \\ \hline \text { 欧氏变换 } & {\left[\begin{array}{cc} \boldsymbol{R} & t \\ 0^{\mathrm{T}} & 1 \end{array}\right]} & 6 & \text { 长度、夹角、体积 } \\ \text { 相似变换 } & {\left[\begin{array}{cc} s \boldsymbol{R} & \boldsymbol{t} \\ \mathbf{0}^{\mathrm{T}} & 1 \end{array}\right]} & 7 & \\ \text { 仿射变换 } & {\left[\begin{array}{cc} \boldsymbol{A} & t \\ 0^{\mathrm{T}} & 1 \end{array}\right]} & 12 & \text { 体积比 } \\ \text { 射影变换 } & {\left[\begin{array}{cc} \boldsymbol{A} & \boldsymbol{t} \\ \boldsymbol{a}^{\mathrm{T}} & v \end{array}\right]} & 15 & \text { 性、体积比 } \\ \hline \end{array}\)
李群&李代数
基础概念
- 群(Group)是集合加上运算的代数结构。
充要性质(丰俭由你):
- 封闭性: $\forall a_1, a_2 \in A, \quad a_1 \cdot a_2 \in A$.
- 结合律: $\forall a_1, a_2, a_3 \in A, \quad\left(a_1 \cdot a_2\right) \cdot a_3=a_1 \cdot\left(a_2 \cdot a_3\right)$.
- 幺元: $\exists a_0 \in A$, s.t. $\forall a \in A, a_0 \cdot a=a \cdot a_0=a$.
- 逆: $\forall a \in A, \quad \exists a^{-1} \in A$, s.t. $a \cdot a^{-1}=a_0$.
- 李群是指具有连续(光滑)性质的群。比如SO\SE,反例:去0的实数乘法群。
李代数
李代数由一个集合$\mathbb{V}$,一个数域$\mathbb{F}$,和一个二元运算符$[,]$(李括号)组成,称 $(\mathbb{V}, \mathbb{F},[,]$,$) 为一个李代数, 记作 \mathfrak{g}$ 。
- 封闭性 $\forall \boldsymbol{X}, \boldsymbol{Y} \in \mathbb{V},[\boldsymbol{X}, \boldsymbol{Y}] \in \mathbb{V}$.
- 双线性 $\forall \boldsymbol{X}, \boldsymbol{Y}, \boldsymbol{Z} \in \mathbb{V}, a, b \in \mathbb{F}$, 有 \([a \boldsymbol{X}+b \boldsymbol{Y}, \boldsymbol{Z}]=a[\boldsymbol{X}, \boldsymbol{Z}]+b[\boldsymbol{Y}, \boldsymbol{Z}], \quad[\boldsymbol{Z}, a \boldsymbol{X}+b \boldsymbol{Y}]=a[\boldsymbol{Z}, \boldsymbol{X}]+b[\boldsymbol{Z}, \boldsymbol{Y}]\)
- 自反性 ${ }^{(2)} \forall \boldsymbol{X} \in \mathbb{V},[\boldsymbol{X}, \boldsymbol{X}]=0$.
- 雅可比等价 $\forall \boldsymbol{X}, \boldsymbol{Y}, \boldsymbol{Z} \in \mathbb{V},[\boldsymbol{X},[\boldsymbol{Y}, \boldsymbol{Z}]]+[\boldsymbol{Z},[\boldsymbol{X}, \boldsymbol{Y}]]+[\boldsymbol{Y},[\boldsymbol{Z}, \boldsymbol{X}]]=\mathbf{0}$.
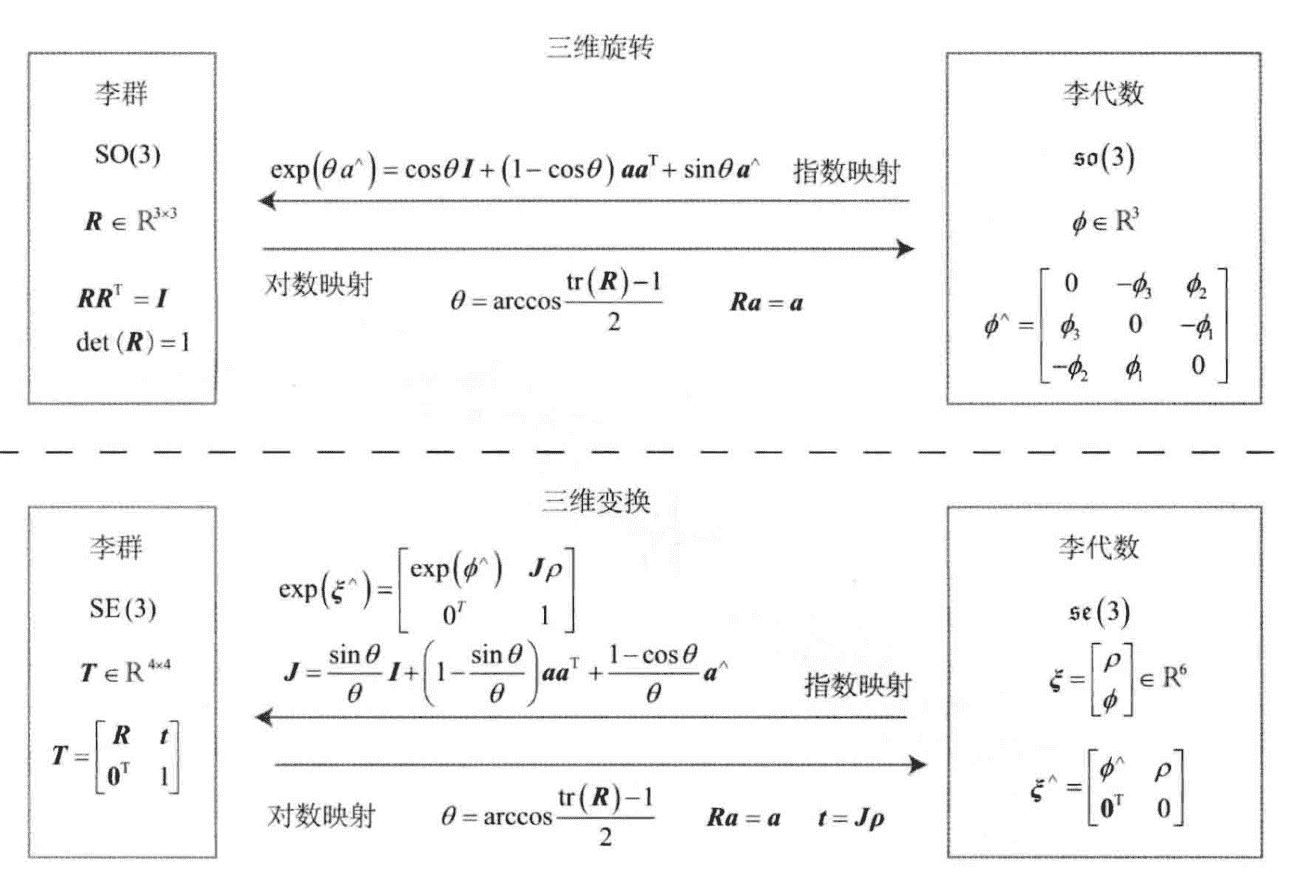
李代数 \(\mathfrak{s o}(3)\)
\(\mathfrak{s o}(3) = (\left\{\boldsymbol{\phi} \in \mathbb{R}^3, \boldsymbol{\Phi}=\boldsymbol{\phi}^{\wedge} \in \mathbb{R}^{3 \times 3}\right\},实数 R, \left[\phi_1, \phi_2\right]=\left(\boldsymbol{\Phi}_1 \boldsymbol{\Phi}_2-\boldsymbol{\Phi}_2 \boldsymbol{\Phi}_1\right)^{\vee})\)
与旋转矩阵$SO(3)$的关系: \(\boldsymbol{R}(t)=\exp \left(\phi_0^{\wedge} t\right)\)
李代数 \(\mathfrak{s e}(3)\)
\[\mathfrak{s e}(3)= (\left\{\boldsymbol{\xi}=\left[\begin{array}{l}\rho \\ \phi\end{array}\right] \in \mathbb{R}^6, \boldsymbol{\rho} \in \mathbb{R}^3, \phi \in \mathfrak{s o}(3), \boldsymbol{\xi}^{\wedge}=\left[\begin{array}{ll}\phi^{\wedge} & \rho \\ \mathbf{0}^{\mathrm{T}} & 0\end{array}\right] \in \mathbb{R}^{4 \times 4}\right\},实数 R,$\left[\boldsymbol{\xi}_1, \boldsymbol{\xi}_2\right]=\left(\boldsymbol{\xi}_1^{\wedge} \boldsymbol{\xi}_2^{\wedge}-\boldsymbol{\xi}_2^{\wedge} \boldsymbol{\xi}_1^{\wedge}\right)^{\vee}$)\]指数映射、对数映射
$SO(3)$ 指对映射
- 指数映射与Rodrigues类似
- 对数映射
$SE(3)$ 指对映射
- 指数映射
其中, \(\begin{aligned} \sum_{n=0}^{\infty} \frac{1}{(n+1) !}\left(\boldsymbol{\phi}^{\wedge}\right)^n & =\boldsymbol{I}+\frac{1}{2 !} \theta \boldsymbol{a}^{\wedge}+\frac{1}{3 !} \theta^2\left(\boldsymbol{a}^{\wedge}\right)^2+\frac{1}{4 !} \theta^3\left(\boldsymbol{a}^{\wedge}\right)^3+\frac{1}{5 !} \theta^4\left(\boldsymbol{a}^{\wedge}\right)^4 \cdots \\ & =\frac{1}{\theta}\left(\frac{1}{2 !} \theta^2-\frac{1}{4 !} \theta^4+\cdots\right)\left(\boldsymbol{a}^{\wedge}\right)+\frac{1}{\theta}\left(\frac{1}{3 !} \theta^3-\frac{1}{5} \theta^5+\cdots\right)\left(\boldsymbol{a}^{\wedge}\right)^2+\boldsymbol{I} \\ & =\frac{1}{\theta}(1-\cos \theta)\left(\boldsymbol{a}^{\wedge}\right)+\frac{\theta-\sin \theta}{\theta}\left(\boldsymbol{a} \boldsymbol{a}^{\mathrm{T}}-\boldsymbol{I}\right)+\boldsymbol{I} \\ & =\frac{\sin \theta}{\theta} \boldsymbol{I}+\left(1-\frac{\sin \theta}{\theta}\right) \boldsymbol{a}^{\mathrm{T}}+\frac{1-\cos \theta}{\theta} \boldsymbol{a}^{\wedge} \stackrel{\text { def }}{=} \boldsymbol{J} . \end{aligned}\)
- 对数映射可以指数映射右上角矩阵解线性方程得到。
求导模型 & 扰动模型
在 SLAM 中, 我们要估计一个相机的位置和姿态, 该位姿是由 $\mathrm{SO}(3)$ 上的旋转矩阵或 $\mathrm{SE}(3)$ 上的变换矩阵描述的。不妨设某个时刻机器人的位姿为 $\boldsymbol{T}$ 。它观察到了一个世界坐标位于 $\boldsymbol{p}$ 的 点, 产生了一个观测数据 $\boldsymbol{z}$ 。那么, 由坐标变换关系知: \(z=\boldsymbol{T}+\boldsymbol{w}\) 其中 $w$ 为随机噪声。由于它的存在, $z$ 往往不可能精确地满足 $z=\boldsymbol{T} p$ 的关系。所以, 我们通常 会计算理想的观测与实际数据的误差: \(e=z-\boldsymbol{T} \boldsymbol{p}\) 假设一共有 $N$ 个这样的路标点和观测, 于是就有 $N$ 个上式。那么, 对小夢卜进行位姿估计, 相当于寻找一个最优的 $\boldsymbol{T}$, 使得整体误差最小化: \(\min _{\boldsymbol{T}} J(\boldsymbol{T})=\sum_{i=1}^N\left\|\boldsymbol{z}_i-\boldsymbol{T} \boldsymbol{p}_i\right\|_2^2 .\) 求解该问题必须要得到$J$对$T$的导数,由此产生了两种求导模型:
- 用李代数表示姿态,然后根据李代数加法对李代数求导。
- 对李群左乘或右乘微小扰动,然后对该扰动求导,称为左扰动和右扰动模型
Baker-Campbell-Hausdorff 公式
BCH公式用于描述旋转矩阵乘在李群上的对应变换: \(\ln (\exp (\boldsymbol{A}) \exp (\boldsymbol{B}))=\boldsymbol{A}+\boldsymbol{B}+\frac{1}{2}[\boldsymbol{A}, \boldsymbol{B}]+\frac{1}{12}[\boldsymbol{A},[\boldsymbol{A}, \boldsymbol{B}]]-\frac{1}{12}[\boldsymbol{B},[\boldsymbol{A}, \boldsymbol{B}]]+\cdots\) $SO(3)$上BCH的近似表达: \(\ln \left(\exp \left(\phi_1^{\wedge}\right) \exp \left(\phi_2^{\wedge}\right)\right)^{\vee} \approx \begin{cases}J_l\left(\phi_2\right)^{-1} \phi_1+\phi_2 & \text { 当 } \phi_1 \text { 为小量, } \\ J_r\left(\phi_1\right)^{-1} \phi_2+\phi_1 & \text { 当 } \phi_2 \text { 为小量. }\end{cases}\)
\(\boldsymbol{J}_l^{-1}=\frac{\theta}{2} \cot \frac{\theta}{2} \boldsymbol{I}+\left(1-\frac{\theta}{2} \cot \frac{\theta}{2}\right) \boldsymbol{a} \boldsymbol{a}^{\mathrm{T}}-\frac{\theta}{2} \boldsymbol{a}^{\wedge} .\) \(\boldsymbol{J}_r(\boldsymbol{\phi})=\boldsymbol{J}_l(-\boldsymbol{\phi})\)
$SE(3)$上BCH的近似表达:
\[\begin{aligned} \exp \left(\Delta \boldsymbol{\xi}^{\wedge}\right) \exp \left(\boldsymbol{\xi}^{\wedge}\right) & \approx \exp \left(\left(\mathcal{J}_l^{-1} \Delta \boldsymbol{\xi}+\boldsymbol{\xi}\right)^{\wedge}\right) \\ \exp \left(\boldsymbol{\xi}^{\wedge}\right) \exp \left(\Delta \boldsymbol{\xi}^{\wedge}\right) & \approx \exp \left(\left(\mathcal{J}_r^{-1} \Delta \boldsymbol{\xi}+\boldsymbol{\xi}\right)^{\wedge}\right) \end{aligned}\]导数模型
首先,考虑$SO(3)$上的情况。假设我们对一个空间点$p$进行了旋转,得到了$Rp$,但是$SO(3)$上没有加法,因此计算对$R$对应的李代数$\phi$的导数 \(\frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\phi}}=(-\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{J}_l\)
扰动模型
设左扰动的李代数为$\boldsymbol{\varphi}$: \(\begin{aligned} \frac{\partial(\boldsymbol{R} \boldsymbol{p})}{\partial \boldsymbol{\varphi}} & =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\exp \left(\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\boldsymbol{\varphi}} \\ & =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\left(\boldsymbol{I}+\boldsymbol{\varphi}^{\wedge}\right) \exp \left(\boldsymbol{\phi}^{\wedge}\right) \boldsymbol{p}-\exp \left(\phi^{\wedge}\right) \boldsymbol{p}}{\boldsymbol{\varphi}} \\ & =\lim _{\boldsymbol{\varphi} \rightarrow 0} \frac{\varphi^{\wedge} \boldsymbol{R} p}{\boldsymbol{\varphi}}=\lim _{\boldsymbol{\varphi} \rightarrow \mathbf{0}} \frac{-(\boldsymbol{R} \boldsymbol{p})^{\wedge} \boldsymbol{\varphi}}{\boldsymbol{\varphi}}=-(\boldsymbol{R} \boldsymbol{p})^{\wedge} . \end{aligned}\)
- 对$SE(3)$的扰动模型: