[TOC]
目标检测技术 & yolo系列介绍
目标检测技术概况
目标检测技术分类
- Anchor based:要在feature map上生成大量先验框,之后进行减框+精化
- Two-stage:第一阶段提取region proposal,第二阶段精确定位+分类;RCNN,FPN
- One-stage:直接分类和回归;YOLO,SSD,Retina-Net
- Anchor free:速度快
- One-stage:CenterNet、CornerNet、Fcos
目标检测发展历史
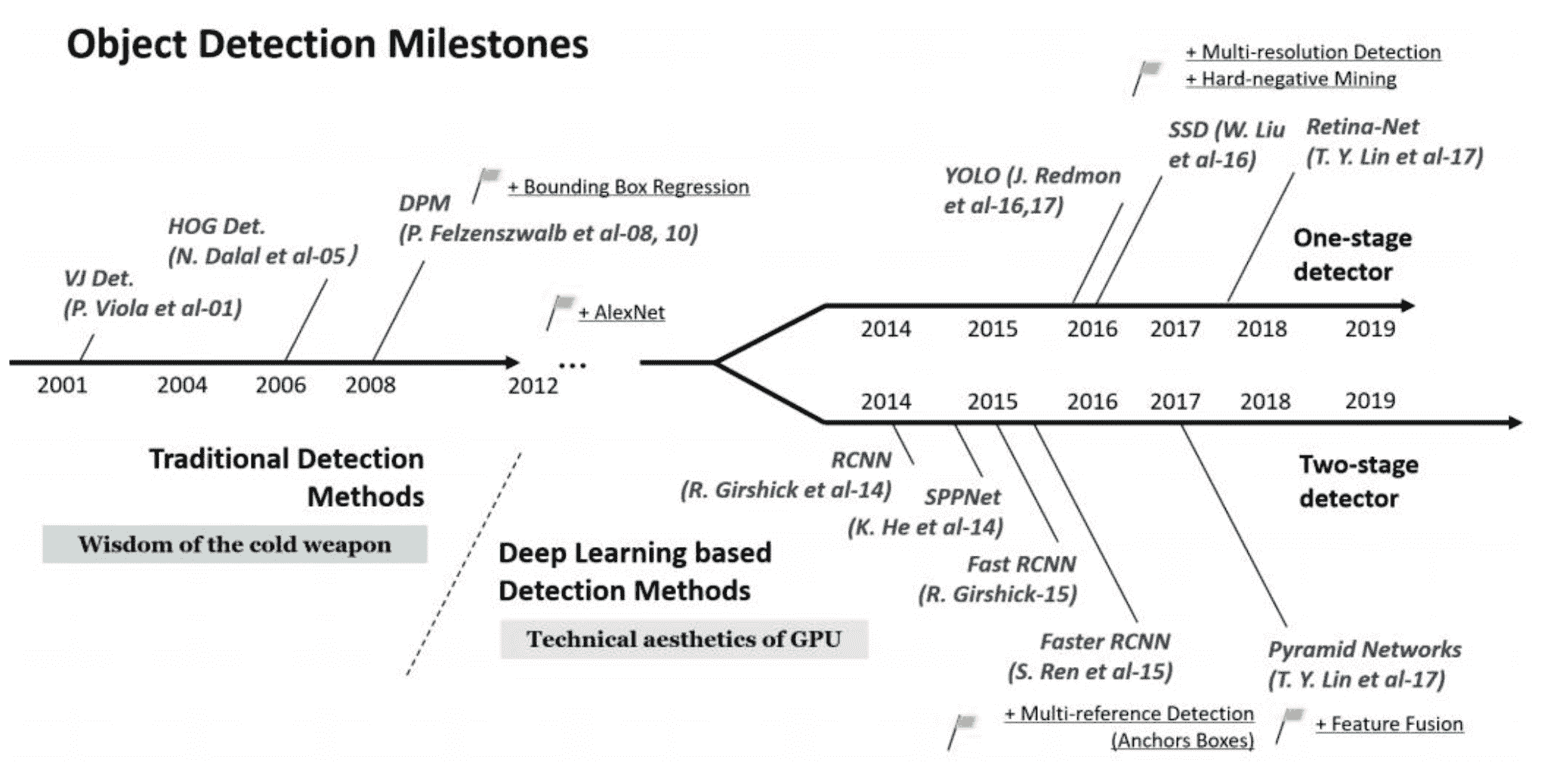
yolo系列目标检测
yolo的原理
-
m x n大小的图像图片m x n x 3 的图片化成 grid-splitted 的点 m1 x n1 x 512(512维度特征,m1、n1小于m、n)
- 每一个1x1的点产生3个anchor
-
对比 anchor 和 ground truth,产生 loss
- 输入与输出:
如果我们有 SxS个框, 每个框的锚框 (bbox) 个数为 $B$, 分类器可以识别出 $C$ 种不同的物体, 那么整个ground truth 的维度为:(其中 5 代表的是每一个anchor需要5个量去描述:中心坐标,长宽,存在目标的置信度) \(\mathrm{S} \times S \times(B \times (5+C))\) 同理, 网络的预测结果的维度也是:
\(\mathrm{S} \times S \times(B \times (5+C))\)
预测结果与GT进行loss计算, loss计算传播更新整 个网络的参数
yolo的意义
- 创造性地将检测和识别合二为一
- 检测速度极快
SOTA的目标检测网络结构
backbone-neck-head:
-
backbone网络对图像特征进行提取
-
neck网络对图像特征进行拼接、变换、融合
-
head网络进行分类与回归
yolo v3算法细节
分类标签上的问题
yolo v3在分类标签上使用的是每一个类别使用逻辑回归(sigmid),而不是使用softmax
在分类模型中用sigmoid和softmax的区别:
在分类模型中,sigmoid和softmax都是用来将模型的输出转化为概率分布,从而用于分类的。
Sigmoid函数可以将任意实数映射到0到1之间的一个值,公式为:
\[sigmoid(x) = \frac{1}{1 + e^{-x}}\]在二分类问题中,sigmoid函数通常被用来将模型输出映射到0到1之间的一个概率值,表示正例的概率。对于多分类问题,可以使用多个sigmoid函数来分别计算每个类别的概率。
相比之下,softmax函数则是将多个实数映射到一个概率分布上。在多分类问题中,softmax函数通常被用来将模型输出转化为每个类别的概率值,公式为:
\[softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^K e^{x_j}}\]其中,$x_i$表示模型对第$i$个类别的得分,$K$表示类别总数。softmax函数可以保证所有类别的概率值之和为1。
因此,sigmoid函数适用于二分类问题或将多分类问题分解成多个二分类问题的情况,而softmax函数适用于多分类问题。
网络结构
- backbone+neck简略概括(输入大小和原文不同):
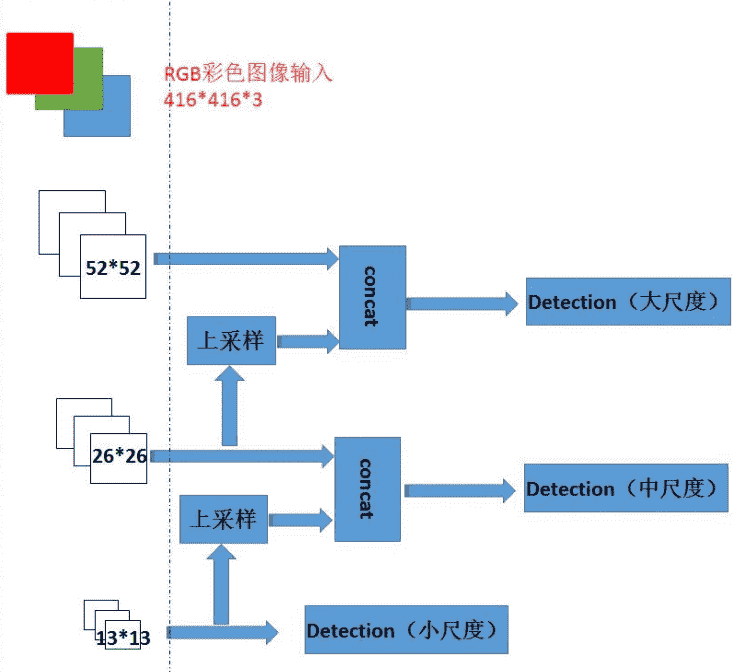
左侧的是backbone网络,提取不同尺度和不同维度的feature map,backbone进行的是下采样,即卷积进行的是下采样。
右侧的是neck网络,用来整合feature map
小尺度的feature map用来检测大尺度目标,大尺度feature map用来检测小尺度目标
concat指的是通道(维度)上的拼接
关于上采样和下采样:
目标检测中的上采样(upsampling)和下采样(downsampling)是指对输入图像进行调整大小的过程,以便将其适应于模型的输入和输出要求。
下采样是指将输入图像的分辨率降低,通常通过对图像进行卷积和池化操作来实现。这种操作可以使模型更快速地处理输入数据,但也会造成信息的丢失。下采样后得到的特征图尺寸通常比输入图像小,但具有更多的抽象信息和语义特征。
上采样是指将特征图的分辨率恢复到原始输入图像的大小,通常通过插值或反卷积等操作来实现。上采样可以恢复图像细节和准确位置信息,使得模型更能够精确地定位目标。在一些目标检测模型中,上采样是通过连接卷积层的不同特征图来实现的,这种方法被称为特征金字塔网络(Feature Pyramid Network,FPN)。
- 输入输出可视化:
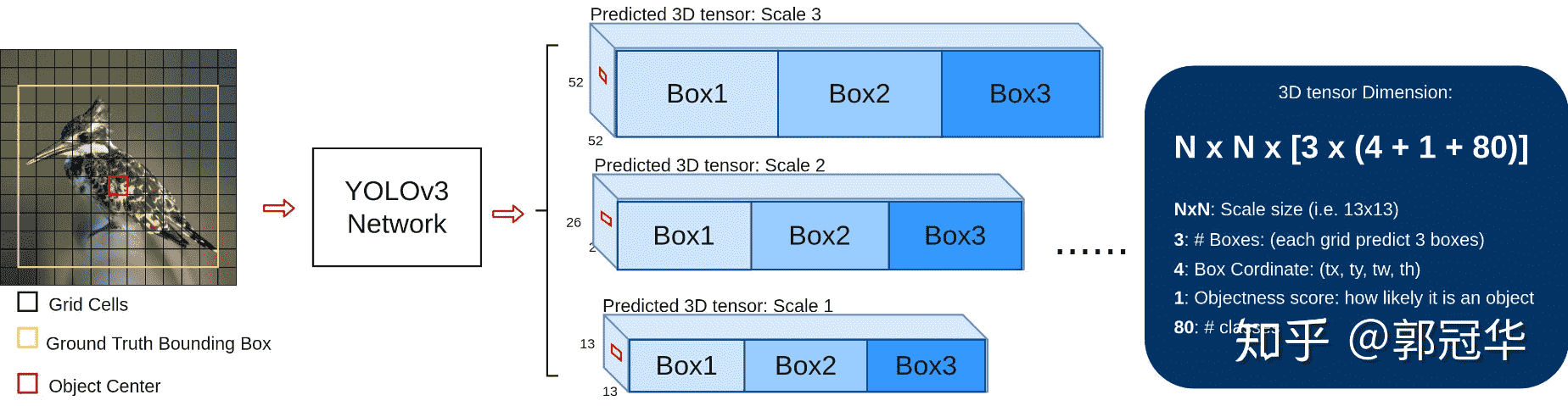
用的是COCO数据集,有80个预测类
- backbone+neck+head标准网络(输入大小和原文一致):
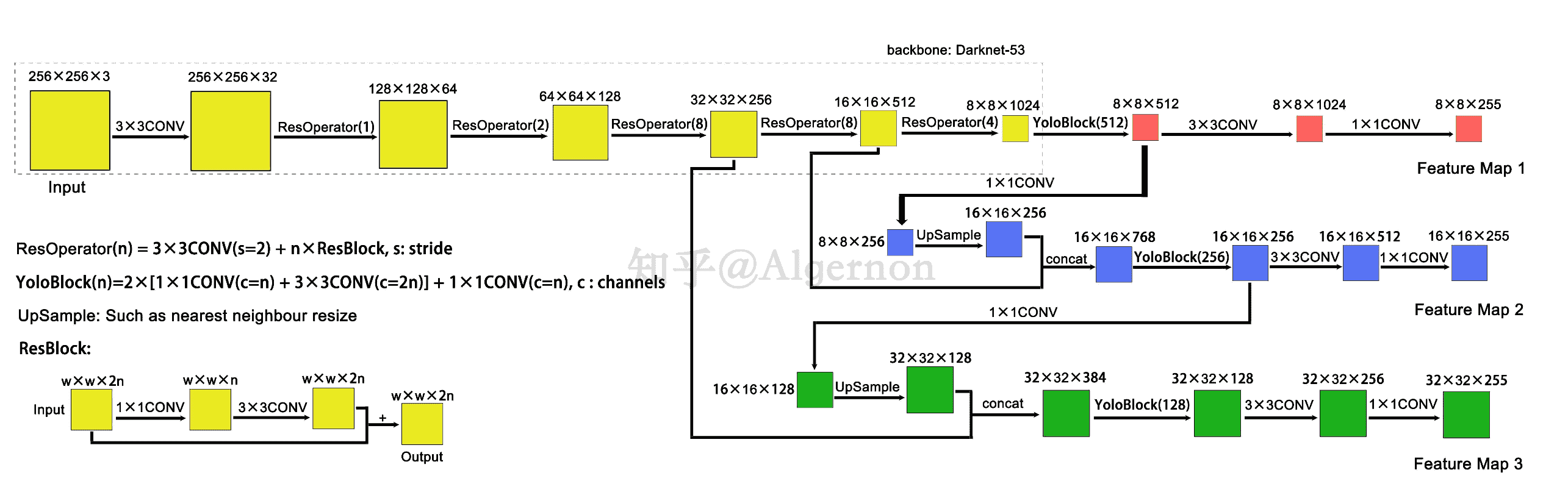
1x1的卷积一般是用来改变通道数的:https://www.zhihu.com/question/56024942
mAP-50(预测与GT的IOU大于0.5判断为正例子)是mAP中的一项
mAP是 mAP-50~mAP-95的平均值
消融实验(ablation study)是指一种科学实验方法,其目的是通过逐步移除某个系统的组成部分来研究它们对系统整体行为的贡献。在机器学习领域中,消融实验常用于研究模型中的各个组件对性能的影响。例如,假设我们有一个分类模型,包括一个卷积神经网络和一个全连接神经网络。为了研究哪个组件对模型性能的贡献更大,我们可以通过消融实验来逐步移除这些组件,比如只使用全连接网络或只使用卷积网络,然后比较模型的性能差异。
三个由backbone提取的特征尺度分别是原图1/8, 1/16, 1/32
-
原文的 yoloBlock 实际上执行了5次卷积
-
darknet没有pooling操作,而特征图的缩减是通过调节卷积步长实现的
输出特征图解码
- 特征图
根据不同的输入尺寸, 会得到不同大小的输出特征图
每个特征图的每个格子中, 都配置3个不同的先验框, 所以最后三个特征图, 这里暂且reshape为8 × 8 × 3 × 85、 16 × 16 × 3 × 85、 32 × 32 × 3 × 85
检测框位置(4维) 、 检测置信度(1维) 、 类别(80维) 都在其中, 加起来正好是85维。
- 先验框
Yolo v3沿用了Yolov2中关于先验框的技巧, 并且使用k-means对数据集中的标签框进行聚类, 得到类别中心点的9个框, 作为先验框。
- 根据先验值&特征图可以调整得到输出框
- 置信度和类别解码
置信度在输出85维中占固定一位, 由sigmoid函数解码即可, 解码之后数值区间在[0, 1]中。
COCO数据集有80个类别, 所以类别数在85维输出中占了80维, 每一维独立代表一个类别的置信度。 使用sigmoid激活函数替代了Yolov2中的softmax, 取消了类别之间的互斥,可以使网络更加灵活。
三个特征图一共可以解码出 8 × 8 × 3 + 16 × 16 × 3 + 32 × 32 × 3 = 4032 个box以及相应的类别、 置信度。 这4032个box, 在训练和推理时, 使用方法不一样:
1)训练时4032个box全部送入打标签函数, 进行后一步的标签以及损失函数的计算。
2)推理时, 选取一个置信度阈值, 过滤掉低阈值box, 再经过nms( 非极大值抑制) , 就可以输出整个网络的预测结果了
训练策略和损失函数
- 训练样本
预测框: 正例( positive) 、 负例( negative) 、 忽略样例( ignore)
先验框数量: 416输入 : 10647个;256输入 : 4032个
正例: 取一个ground truth, 与4032个框全部计算IOU, 最大的为正例。 正例产生置信度loss、 检测框loss、 类别loss。 ground truth box为对应的预测框的标签。
负例: 与全部ground truth的IOU都小于阈值( 0.5) , 则为负例。 负例只有分类置信度产生loss, 分类标签为0, 边框回归不产生loss。
忽略样例: 正例除外, 与任意一个ground truth的IOU大于阈值( 论文中使用0.5) , 则为忽略样例。 忽略样例不产生任何loss。
- 损失函数
x、 y、 w、 h使用MSE作为损失函数, 也可以使用smooth L1 loss : \(M S E=\frac{1}{n} \sum_{i=1}^n\left(y_i-\overline{y_i}\right)^2\) 分类损失先用sigmoid,后计算二元交叉熵: \(\sigma(z)=\frac{1}{1+\mathrm{e}^{-z}}\)
\[\text { Loss }=-\frac{1}{N} \sum_{\mathrm{i}=1}^{\mathrm{N}} \mathrm{y}_{\mathrm{i}} \cdot \log \left(\mathrm{p}\left(\mathrm{y}_{\mathrm{i}}\right)\right)+\left(1-\mathrm{y}_{\mathrm{i}}\right) \cdot \log \left(1-\mathrm{p}\left(\mathrm{y}_{\mathrm{i}}\right)\right)\]