[TOC]
Norm
- L1范数(稀疏规则算子, Lasso regularization): 为x向量各个元素绝对值之和
- L2范数: 为x向量各个元素平方和的1/2次方,L2范数又称Euclidean范数或Frobenius范数
- Lp范数: 为x向量各个元素绝对值p次方和的1/p次方
Lasso regularization是一种用于线性回归模型的正则化方法,它通过在模型的损失函数中添加L1范数惩罚项来惩罚模型中的大型权重,从而避免过拟合。Lasso regularization的数学表达式为:
\[L_{\text{lasso}}(\beta) = \frac{1}{2n} \lVert \mathbf{y} - \mathbf{X}\beta \rVert_2^2 + \alpha \lVert \beta \rVert_1\]其中,$\mathbf{y}$是目标变量向量,$\mathbf{X}$是特征矩阵,$\beta$是模型的权重向量,$n$是样本数量,$\alpha$是正则化强度超参数。L1范数惩罚项$\lVert \beta \rVert_1$可以促使模型中的某些权重变为0,从而实现特征选择的效果。
而Lasso loss是指Lasso回归模型的损失函数,它是由数据集中的观测值与Lasso regularization的总和构成的。Lasso loss的数学表达式为:
\[L_{\text{lasso}}(\beta) = \frac{1}{2n} \sum_{i=1}^n (y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 + \alpha \sum_{j=1}^p \lvert \beta_j \rvert\]其中,$y_i$是第$i$个观测值的目标变量,$x_{ij}$是第$i$个观测值的第$j$个特征,$\beta_0$是模型的截距,$\beta_j$是模型的第$j$个权重,$n$是样本数量,$p$是特征数量,$\alpha$是正则化强度超参数。L1范数惩罚项$\sum_{j=1}^p \lvert \beta_j \rvert$可以促使模型中的某些权重变为0,从而实现特征选择的效果。
- 对比:
- L1范数可以使权值稀疏,方便特征提取。(使得不重要的特征权重为0,反之不为0)https://lcqbit11.blog.csdn.net/article/details/103101607
- L2范数可以防止过拟合,提升模型的泛化能力。
- L1倾向选择更少特征,使得其他特征权重为0;L2选择更多特征,使得权重接近于0。
Overfitting 产生原因
- 数据量太小 or 噪声太大
- trainset和testset数据分布不一致
- 模型复杂度太大
-
过度训练
- 解决方法:
- 正则化(正则化可以限制模型的复杂度) or dropout
- 交叉验证 or 创建一个验证集
- 特征选择/特征降维
- 数据集扩增
- 降低模型复杂度
- batch normalizatin
Decision Tree
- ID3 算法的核心是在决策树的每个节点上应用信息增益准则选择特征,递归地构架决策树。
- C4.5 算法的核心是在生成过程中用信息增益比来选择特征。
- CART 树算法的核心是在生成过程用基尼指数来选择特征。
基于决策树的算法有随机森林、GBDT、Xgboost 等。
梯度问题
1.梯度消失: 根据链式法则,如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话,那么即使这个结果是0.99,在经过足够多层传播之后,误差对输入层的偏导会趋于0。
可以采用ReLU激活函数有效的解决梯度消失的情况。(ReLU函数在输入值大于0时,导数恒为1,这意味着反向传播时梯度不会消失。)
2.梯度膨胀: 根据链式法则,如果每一层神经元对上一层的输出的偏导乘上权重结果都大于1的话,在经过足够多层传播之后,误差对输入层的偏导会趋于无穷大。
可以通过激活函数来解决。
3.梯度爆炸: 针对梯度爆炸问题,解决方案是引入Gradient Clipping(梯度裁剪)。
通过Gradient Clipping,将梯度约束在一个范围内,这样不会使得梯度过大。
AUC 是怎么计算的
-
1)最直观的,根据 AUC 这个名称,我们知道,计算出 ROC 曲线下面的面积,就是 AUC 的值。事实上,这也是在早期 Machine Learning 文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的 AUC 曲线必然是一个阶梯状的。因此,计算的 AUC 也就是这些阶梯下面的面积之和。
这样,我们先把 score 排序(假设 score 越大,此样本属于正类的概率越大),然后一边扫描就可以得到我们想要的 AUC。但是,这么 做有个缺点,就是当多个测试样本的 score 相等的时候,我们调整一下阈值,得到的不是曲线一个阶梯往上或者往右的延展,而是斜着向上形成一个梯形。
此时,我们就需要计算这个梯形的面积。由此,我们可以看到,用这种方法计算 AUC 实际上是比较麻烦的。
-
2)一个关于AUC的很有趣的性质是,它和 Wilcoxon-Mann-Witney Test (Mann Witney U test )是等价的。而 Wilcoxon-Mann-Witney Test 就是测试任意给一个正类样本和一个负类样本,正类样本的 score 有多大的概率大于负类样本的 score。有了这个定义,我们就得到了另外一中计算 AUC 的办法:得到这个概率。 我们知道,在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。
这和上面的方法中,样本数越多,计算的 AUC 越准确类似,也和计算积分的时候,小区间划分的越细,计算的越准确是同样的道理。具体来说就是统计一下所有的 M×N(M为正类样本的数目,N为负类样本的数目)个正负样本对中,有多少个组中的正样本的 score 大于负样本的score。
当二元组中正负样本的 score相等的时候,按照 0.5 计算。然后除以 MN。实现这个方法的复杂度为 O(n^2)。n 为样本数(即 n=M+N )
-
3) 第三种方法实际上和上述第二种方法是一样的,但是复杂度减小了。它也是首先对 score 从大到小排序,然后令最大 score 对应的 sample 的 rank 为n,第二大 score 对应 sample 的 rank 为n-1,以此类推。然后把所有的正类样本的 rank 相加,再减去 M-1 种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的 score 大于负类样本的 score。然后再除以 M×N。即
公式解释:
1.为了求的组合中正样本的 score 值大于负样本,如果所有的正样本 score 值都是大于负样本的,那么第一位与任意的进行组合 score 值都要大,我们取它的 rank 值为 n,但是 n-1 中有 M-1 是正样例和正样例的组合这种是不在统计范围内的(为计算方便我们取n组,相应的不符合的有 M 个),所以要减掉,那么同理排在第二位的 n-1,会有 M-1 个是不满足的,依次类推,故得到后面的公式 M*(M+1)/2,我们可以验证在正样本 score 都大于负样本的假设下,AUC 的值为1
2.根据上面的解释,不难得出,rank 的值代表的是能够产生 score 前大后小的这样的组合数,但是这里包含了(正,正)的情况,所以要减去这样的组(即排在它后面正例的个数),即可得到上面的公式。
另外,特别需要注意的是,再存在 score 相等的情况时,对相等 score 的样本,需要 赋予相同的 rank (无论这个相等的 score 是出现在同类样本还是不同类的样本之间,都需要这样处理)。具体操作就是再把所有这些 score 相等的样本 的rank取平均。然后再使用上述公式。
假设检验与p-value
当我们将样本中得到的结果推论到总体时,如果样本恰好只是个别现象,或者样本数目过少时,就会出现误差。所以我们就可以提出一个假设 (Hypothesis) ,假设样本的结果可以推论到总体,而检验这个假设是否靠得住就可以通过统计学家们提出的检验方法来计算得出,这些检验方法就包括了 T检验、F检验、卡方检验等,通过这些检验的方法得到的检验统计量,我们就可以进一步计算出在假设为真时,样本结果出现的概率,这样我们就可以在知道有多少的概率接受或者拒绝原假设了。 另外,每种假设检验的方法都有它们的应用场景和使用条件,所以还是要根据实际情况来选择合适的检验方法。
-
P值 (P-value)
P值,也就是常见到的 P-value。P 值是一种概率,指的是在 H0 假设为真的前提下,样本结果出现的概率。如果 P-value 很小,则说明在原假设为真的前提下,样本结果出现的概率很小,甚至很极端,这就反过来说明了原假设很大概率是错误的。通常,会设置一个显著性水平(significance level) α 与 P-value 进行比较,如果 P-value < α ,则说明在显著性水平 α 下拒绝原假设,α 通常情况下设置为0.05。
-
T检验 (T-test)
T检验,也称为 student t 检验 (Student’s t test),用于对两个总体均值差的检验,因为当 F 分布在自由度趋向于无穷大时,近似于正态分布,所以 T 检验通常用于两个正态分布均值差的检验。 T统计量 (T-statistic) 是 T-test 做假设检验时用到的检验统计量,通过 T-statistic 的值可以计算出 P-value,从而判断是否拒绝原假设。
-
卡方检验 (chi-square test)
卡方检验有两种基本类型:独立性检验和拟合度检验(Goodness-of-fit test),本质上都是样本频度和期望频度之间计算统计量
卡方检验,主要用于检验统计样本的实际观测值与理论推断值之间的偏离程度,或者是检验一批数据是否与某种理论分布相符合。 卡方值是卡方检验时用到的检验统计量,卡方值越大,说明观测值与理论值之间的偏离就越大;反之,二者偏差越小。实际应用时,可以根据卡方值计算 P-value,从而选择拒绝或者接受原假设。
-
卡方独立性检验
卡方独立性检验是一种统计方法,用于检验两个分类变量之间是否独立。在卡方独立性检验中,我们将观察到的数据与期望的数据进行比较,以确定两个变量之间是否存在显著的关联。
在进行卡方独立性检验时,我们需要先计算出期望的数据。这可以通过将每个分类变量的边际分布相乘,然后除以总数来实现。然后,我们可以使用以下公式计算卡方统计量:
$\chi^2 = \sum_{i=1}^n \sum_{j=1}^m \frac{(O_{ij} - E_{ij})^2}{E_{ij}}$
其中,$O_{ij}$ 是观察到的频数,$E_{ij}$ 是期望的频数,$n$ 和 $m$ 分别是两个分类变量的类别数。
最后,我们将卡方统计量与自由度为 $(n-1)(m-1)$ 的卡方分布进行比较,以确定两个变量之间是否存在显著的关联。如果卡方统计量大于临界值,则我们可以拒绝原假设,即两个变量之间不存在关联。如果卡方统计量小于临界值,则我们无法拒绝原假设,即两个变量之间可能存在关联。
在实际应用中,我们可以使用各种统计软件来执行卡方独立性检验,如 R 语言中的 chisq.test() 函数。
- 卡方拟合度检验
卡方拟合度检验(Chi-square goodness-of-fit test)是一种用于检验一个样本数据是否符合一个特定的理论分布的假设检验方法。该方法通常用于检验一个样本数据是否符合正态分布、泊松分布、指数分布等常见的概率分布。
在卡方拟合度检验中,我们需要先确定一个假设的分布,并计算出在该分布下每个区间的期望频数。然后我们需要将观察到的频数与期望频数进行比较,计算出卡方统计量,其计算公式如下:
$\chi^2 = \sum_{i=1}^n \sum_{j=1}^m \frac{(O_{ij} - E_{ij})^2}{E_{ij}}$
其中,$O_{ij}$ 是观察到的频数,$E_{ij}$ 是期望的频数,$n$ 和 $m$ 分别是两个分类变量的类别数。
然后我们需要计算P值,其计算方法与独立性检验类似,通过查卡方分布表来确定P值。如果P值小于预先设定的显著性水平(通常为0.05或0.01),则拒绝原假设,即拒绝该样本符合该理论分布的假设。否则,不能拒绝原假设,即该样本数据符合该理论分布的假设。
需要注意的是,在进行卡方拟合度检验时,要确保样本数据满足一定的条件,如样本数据应该是来自于一个简单随机样本、每个观测值之间应该是独立的、样本数据应该足够大等。如果不满足这些条件,就可能导致卡方检验的结果不准确。
内置sqrt
def sqrt(x):
if x == 0:
return 0
# 初始猜测值为x
guess = x
while True:
# 使用牛顿迭代法计算下一个猜测值
new_guess = 0.5 * (guess + x / guess)
# 如果新的猜测值与上一个猜测值非常接近,就认为已经收敛了
if abs(new_guess - guess) < 1e-9:
break
guess = new_guess
return guess
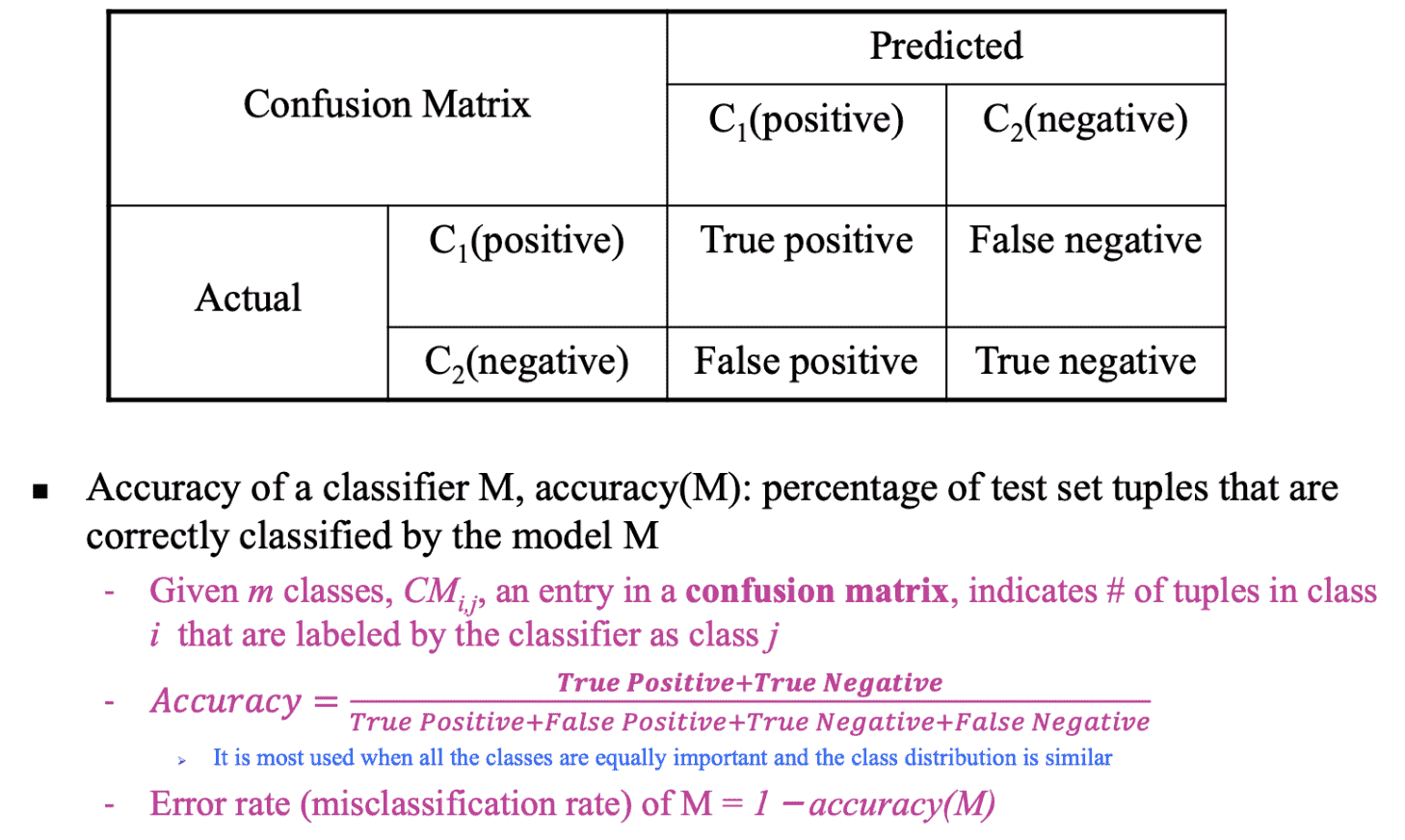
评价指标

神经网络初始化
https://blog.csdn.net/u012328159/article/details/80025785
PCA
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#计算均值,要求输入数据为numpy的矩阵格式,行表示样本数,列表示特征
def meanX(dataX):
return np.mean(dataX,axis=0)#axis=0表示依照列来求均值。假设输入list,则axis=1
def pca(XMat, k):
"""
XMat:传入的是一个numpy的矩阵格式,行表示样本数,列表示特征
k:表示取前k个特征值相应的特征向量
finalData:指的是返回的低维矩阵
reconData:相应的是移动坐标轴后的矩阵
"""
average = meanX(XMat)
m, n = np.shape(XMat)
data_adjust = []
avgs = np.tile(average, (m, 1))
data_adjust = XMat - avgs
covX = np.cov(data_adjust.T) #计算协方差矩阵
featValue, featVec= np.linalg.eig(covX) #求解协方差矩阵的特征值和特征向量
index = np.argsort(-featValue) #依照featValue进行从大到小排序
finalData = []
if k > n:
print("k must lower than feature number")
return
else:
#注意特征向量时列向量。而numpy的二维矩阵(数组)a[m][n]中,a[1]表示第1行值
selectVec = np.matrix(featVec.T[index[:k]]) #所以这里须要进行转置
finalData = data_adjust * selectVec.T
reconData = (finalData * selectVec) + average
return finalData, reconData