machine learning

precision-recall

precision-recall cookbook

Posted by Kylin on April 21, 2023

[TOC]

ROC (Receiver Operating Characteristic) 曲线

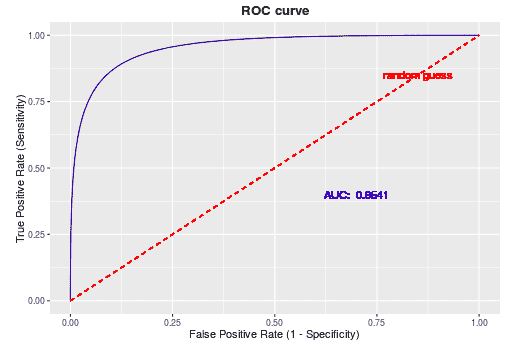
v2-7a45780df4c9930f04d8541b98f70d54_1440w

ROC曲线常用于二分类问题中的模型比较, 主要表现为一种真阳率 (TPR) 和假阳率 (FPR) 的平衡。具体方法是在不同的分类阈值 (threshold) 设定下分别以TPR和FPR为纵、横轴作图。由 ROC曲线的两个指标, $T P R=\frac{T P}{P}=\frac{T P}{T P+F N}, \quad F P R=\frac{F P}{N}=\frac{F P}{F P+T N}$ 可以看出, 当一个样本被分类器判为正例, 若其本身是正例, 则TPR增加; 若其本身是负例, 则FPR增加, 因此ROC曲线可以看作是随着阈值的不断移动, 所有样本中正例与负例之间的”对抗”。曲线越靠近左上角，意味着越多的正例优先于负例，模型的整体表现也就越好。

AUC反映的是分类器对样本的排序能力，依照上面的例子就是A排在B前面的概率。AUC越大，自然排序能力越好，即分类器将越多的正例排在负例之前。

ROC曲线的绘制方法

假设有 $\mathrm{P}$ 个正例, $\mathrm{N}$ 个反例, 首先拿到分类器对于每个样本预测为正例的概 率, 根据概率对所有样本进行逆序排列, 然后将分类阈值设为最大, 即把所有样本均预测为反例, 此时图上的点为 $(0,0)$ 。然后将分类阈值依次设为每个样本的预测概率, 即依次将每个样本划分为 正例, 如果该样本为真正例, 则 $\mathrm{TP}+1$, 即 $T P R+\frac{1}{P}$; 如果该样本为负例, 则 $\mathrm{FP}+1$, 即 $F P R+\frac{1}{N}$ 。最后的到所有样本点的TPR和FPR值, 用线段相连。

ROC的特点

v2-5b2e1966e5a1c06f050ad5954de9a1f5_1440w

$\mathrm{ROC}$ 曲线两个指标, $T P R=\frac{T P}{P}=\frac{T P}{T P+F N}, F P R=\frac{F P}{N}=\frac{F P}{F P+T N}$

注意TPR用到的TP和FN同属P列，FPR用到的FP和TN同属N列，所以即使P或N的整体数量发生了改变，也不会影响到另一列。也就是说，即使正例与负例的比例发生了很大变化，ROC曲线也不会产生大的变化，而像Precision使用的TP和FP就分属两列，则易受类别分布改变的影响。

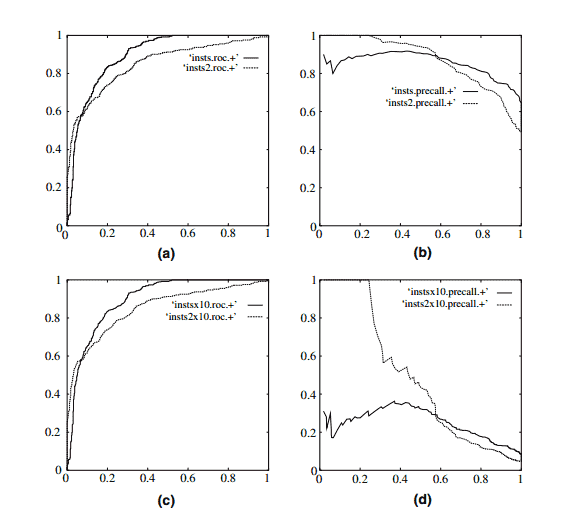
参考文献 [1] 中举了个例子，负例增加了10倍，ROC曲线没有改变，而PR曲线则变了很多。作者认为这是ROC曲线的优点，即具有鲁棒性，在类别分布发生明显改变的情况下依然能客观地识别出较好的分类器。

v2-8a7193b79c60ed91e5b6fa4f865b19cd_1440w

AUC (Area Under Curve)

即ROC曲线下面积。以下介绍计算方式：

  • 1）最直观的，根据 AUC 这个名称，我们知道，计算出 ROC 曲线下面的面积，就是 AUC 的值。事实上，这也是在早期 Machine Learning 文献中常见的AUC计算方法。由于我们的测试样本是有限的。我们得到的 AUC 曲线必然是一个阶梯状的。因此，计算的 AUC 也就是这些阶梯下面的面积之和。

    这样，我们先把 score 排序(假设 score 越大，此样本属于正类的概率越大)，然后一边扫描就可以得到我们想要的 AUC。但是，这么 做有个缺点，就是当多个测试样本的 score 相等的时候，我们调整一下阈值，得到的不是曲线一个阶梯往上或者往右的延展，而是斜着向上形成一个梯形。

    此时，我们就需要计算这个梯形的面积。由此，我们可以看到，用这种方法计算 AUC 实际上是比较麻烦的。

  • 一个关于AUC的很有趣的性质是，它和 Wilcoxon-Mann-Witney Test (Mann Witney U test) 是等价的。而 Wilcoxon-Mann-Witney Test 就是测试任意给一个正类样本和一个负类样本，正类样本的 score 有多大的概率大于负类样本的 score。有了这个定义，我们就得到了另外一中计算 AUC 的办法：得到这个概率。 我们知道，在有限样本中我们常用的得到概率的办法就是通过频率来估计之。这种估计随着样本规模的扩大而逐渐逼近真实值。

    这和上面的方法中，样本数越多，计算的 AUC 越准确类似，也和计算积分的时候，小区间划分的越细，计算的越准确是同样的道理。具体来说就是统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的 score 大于负样本的score。

    当二元组中正负样本的 score相等的时候，按照 0.5 计算。然后除以 MN。实现这个方法的复杂度为 O(n^2)。n 为样本数（即 n=M+N ）

  • 第三种方法实际上和上述第二种方法是一样的，但是复杂度减小了。它也是首先对 score 从大到小排序，然后令最大 score 对应的 sample 的 rank 为n，第二大 score 对应 sample 的 rank 为n-1，以此类推。然后把所有的正类样本的 rank 相加，再减去 M-1 种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的 score 大于负类样本的 score。然后再除以 M×N。即

\[A U C=\frac{\sum_{\text {ie postitleClass }} \operatorname{rank}_i-\frac{M(1+M)}{2}}{M \times N}\]

公式解释：

1.为了求的组合中正样本的 score 值大于负样本，如果所有的正样本 score 值都是大于负样本的，那么第一位与任意的进行组合 score 值都要大，我们取它的 rank 值为 n，但是 n-1 中有 M-1 是正样例和正样例的组合这种是不在统计范围内的（为计算方便我们取n组，相应的不符合的有 M 个），所以要减掉，那么同理排在第二位的 n-1，会有 M-1 个是不满足的，依次类推，故得到后面的公式 M*(M+1)/2，我们可以验证在正样本 score 都大于负样本的假设下，AUC 的值为1

2.根据上面的解释，不难得出，rank 的值代表的是能够产生 score 前大后小的这样的组合数，但是这里包含了（正，正）的情况，所以要减去这样的组（即排在它后面正例的个数），即可得到上面的公式。

另外，特别需要注意的是，再存在 score 相等的情况时，对相等 score 的样本，需要 赋予相同的 rank (无论这个相等的 score 是出现在同类样本还是不同类的样本之间，都需要这样处理)。具体操作就是再把所有这些 score 相等的样本 的rank取平均。然后再使用上述公式。

PR曲线

PR曲线展示的是Precision vs Recall的曲线，PR曲线与ROC曲线的相同点是都采用了TPR (Recall)，都可以用AUC来衡量分类器的效果。不同点是ROC曲线使用了FPR，而PR曲线使用了Precision，因此PR曲线的两个指标都聚焦于正例。类别不平衡问题中由于主要关心正例，所以在此情况下PR曲线被广泛认为优于ROC曲线。

AUPRC (Area Under the PR Curve，AP 即 Average Precision)

PR曲线的绘制与ROC曲线类似，PR曲线的AUC面积计算公式为： \(\sum_n\left(R_n-R_{n-1}\right) P_n\)

目标检测中的 mAP

mAP（mean Average Precision）是目标检测算法中用于评价模型性能的指标之一。它衡量了模型对不同目标类别的检测精度以及对检测结果进行排序的能力。一般来说，mAP越高，模型的性能越好。

mAP的计算方法与目标检测算法使用的评价指标有关，下面介绍一种常见的计算方法：

  1. 对于每个目标类别，根据检测结果进行排序，将检测结果按照置信度从高到低排序；
  2. 根据排序结果（从高到低调整阈值，这样recall是稳定增加到，而precision不一定增加或减少），计算Precision-Recall曲线。Precision表示检测到的目标中真正属于该类别的比例，Recall表示真实属于该类别的目标被检测出来的比例。Precision-Recall曲线就是在不同的Recall下，对应的Precision值组成的曲线；
  3. 计算AP（Average Precision）。对于每个类别，将Precision-Recall曲线下的面积作为AP。
  4. 计算mAP。将所有类别的AP求平均值即为mAP。

例如，一个模型在三个类别上的AP分别为0.8、0.7和0.6，则该模型的mAP为(0.8+0.7+0.6)/3=0.7。

在计算过程中，如果遇到某个类别没有检测结果，导致Precision的分母（TP + FP）为 0，可以采取以下方法解决：

  1. 在计算Precision时，将0/0的情况视为1，即认为没有检测结果的类别Precision为1。这种情况下，mAP可能高于实际性能，因为没有检测到的类别不会对评价指标产生负面影响。
  2. 忽略这个类别，只计算其他类别的AP。这种情况下，mAP可能低于实际性能，因为没有检测到的类别会对评价指标产生负面影响。

为了得到稳定的曲线，从右到左对Precision进行插值：对于每个Recall值，取其右侧最大的Precision值。

使用场景

  1. ROC曲线由于兼顾正例与负例，所以适用于评估分类器的整体性能，相比而言PR曲线完全聚焦于正例。
  2. 如果有多份数据且存在不同的类别分布，比如信用卡欺诈问题中每个月正例和负例的比例可能都不相同，这时候如果只想单纯地比较分类器的性能且剔除类别分布改变的影响，则ROC曲线比较适合，因为类别分布改变可能使得PR曲线发生变化时好时坏，这种时候难以进行模型比较；反之，如果想测试不同类别分布下对分类器的性能的影响，则PR曲线比较适合。
  3. 如果想要评估在相同的类别分布下正例的预测情况，则宜选PR曲线。
  4. 类别不平衡问题中，ROC曲线通常会给出一个乐观的效果估计，所以大部分时候还是PR曲线更好。
  5. 最后可以根据具体的应用，在曲线上找到最优的点，得到相对应的precision，recall，f1 score等指标，去调整模型的阈值，从而得到一个符合具体应用的模型。

AUC vs AP

当正负例不平衡时，可能会出现AUC估计偏高

  • eg.

真实标签：[1, 1, 0, 0, 0, 0, 0, 0, 0, 0]

预测概率：[0.92, 0.4, 0.9, 0.89, 0.88, 0.87, 0.86, 0.85, 0.84, 0.1]

AUC计算：

我们可以计算出以下阈值对应的 TPR 和 FPR：

阈值 > 0.92: TPR = 0/2 = 0, FPR = 0/8 = 0
阈值 > 0.9: TPR = 1/2 = 0.5, FPR = 0/8 = 0
阈值 > 0.4: TPR = 1/2 = 0.5, FPR = 7/8 = 0.875
阈值 > 0.1: TPR = 2/2 = 1, FPR = 7/8 = 0.875
阈值 <= 0.1: TPR = 2/2 = 1, FPR = 8/8 = 1
然后我们可以绘制 ROC 曲线并计算 AUC：

ROC 曲线上的点坐标：
(0, 0) -> (0, 0.5) -> (0.875, 0.5) -> (0.875, 1) -> (1, 1)

ROC 曲线下的面积可以通过计算梯形面积得到：
AUC = 0.5 * (0.5 - 0) * (0.875 - 0) + (0.875 - 0) * (1 - 0.5) = 0.21875 + 0.4375 = 0.65625

AP计算：

对于 AP（Precision-Recall 曲线下的面积），我们需要计算不同的 Recall 水平下的 Precision：

Recall 1/2: Precision = 1/1 = 1.00
Recall 2/2: Precision = 2/10 = 0.20

将这些 Precision 值平均起来，我们得到 AP 值为 0.6。

Reference:

  1. Tom Fawcett. An introduction to ROC analysis
CATALOG
    FEATURED TAGS
    From Bohemia Linux Git Cloud Computer Architecture Database machine learning paper software coding quant Object Detection job programming Competition lecture nlp competition llmsys
    FRIENDS