[TOC]
差分数组
举例
考虑数组 $a=[1,3,3,5,8]$ ,对其中的相邻元素两两作差(右边减左边),得到数组 $[2,0,2,3]$ 。然后在开头补上 $a[0]$ ,得到差分数组
\[d=[1,2,0,2,3]\]这有什么用呢? 如果从左到右累加 $d$ 中的元素,我们就「还原」回了 $a$ 数组 $[1,3,3,5,8]$ 。这类似求导与积分的概念。
这又有什么用呢? 现在把连续子数组 $a[1], a[2], a[3]$ 都加上 10 ,得到 $a^{\prime}=$ $[1,13,13,15,8]$ 。再次两两作差,并在开头补上 $a^{\prime}[0]$ ,得到差分数组 \(d^{\prime}=[1,12,0,2,-7]\)
对比 $d$ 和 $d^{\prime}$ ,可以发现只有 $d[1]$ 和 $d[4]$ 变化了,这意味着对 $a$ 中连续子数组的操作,可以转变成对差分数组 $d$ 中两个数的操作。
定义和性质
对于数组 $a$ ,定义其差分数组 (difference array) 为 \(d[i]= \begin{cases}a[0], & i=0 \\ a[i]-a[i-1], & i \geq 1\end{cases}\)
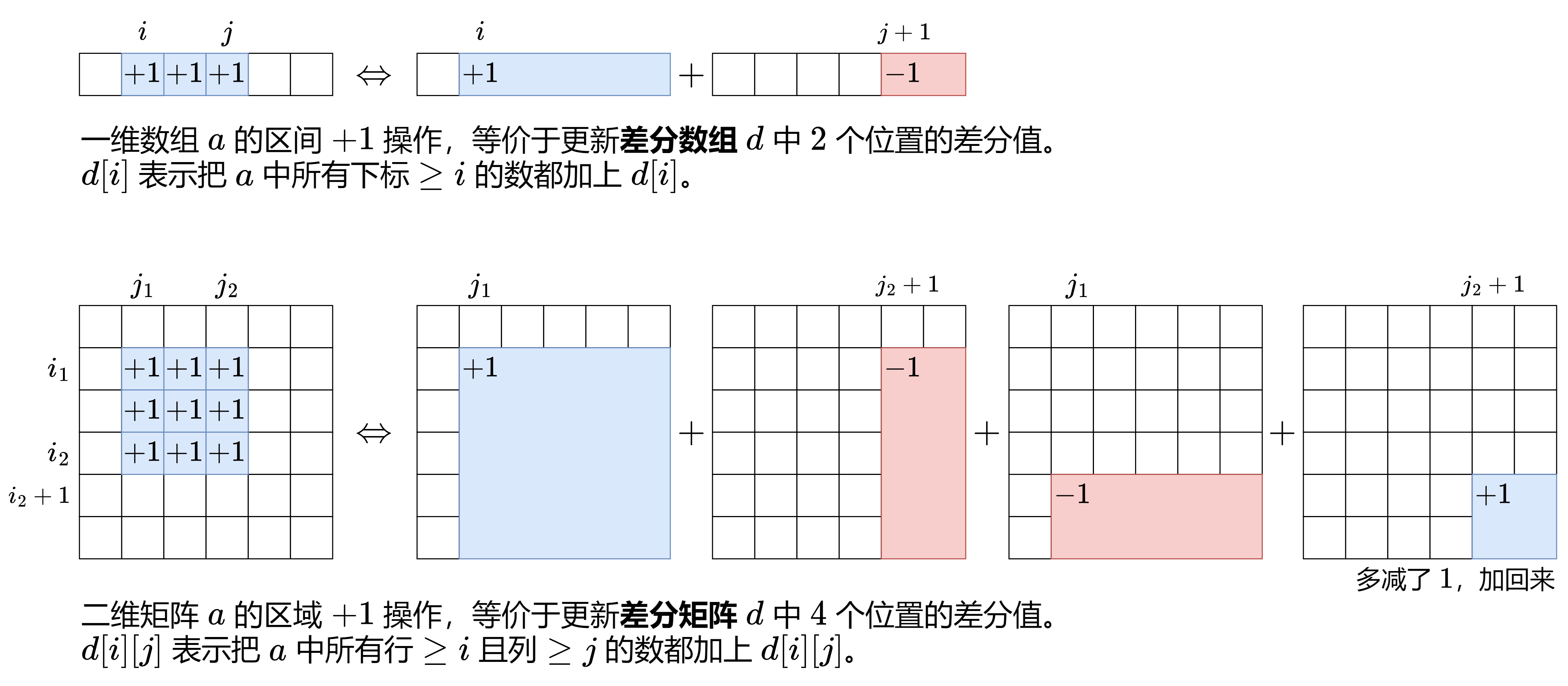
性质 1: 从左到右累加 $d$ 中的元素,可以得到数组 $a$ 。 性质 2: 如下两个操作是等价的。
- 把 $a$ 的子数组 $a[i], a[i+1], \cdots, a[j]$ 都加上 $x$ 。
- 把 $d[i]$ 增加 $x$ ,把 $d[j+1]$ 减少 $x$ 。
利用性质 2,我们只需要 $\mathcal{O}(1)$ 的时间就可以完成对 $a$ 的子数组的操作。最后利用性质 1 从差分数组复原出数组 $a$ 。
注: 也可以这样理解, $d[i]$ 表示把下标 $\geq i$ 的数都加上 $d[i]$ 。
e.g., leetcode 1094
车上最初有 capacity 个空座位。车 只能 向一个方向行驶(也就是说,不允许掉头或改变方向)
给定整数 capacity 和一个数组 trips , trip[i] = [numPassengersi, fromi, toi] 表示第 i 次旅行有 numPassengersi 乘客,接他们和放他们的位置分别是 fromi 和 toi 。这些位置是从汽车的初始位置向东的公里数。
当且仅当你可以在所有给定的行程中接送所有乘客时,返回 true,否则请返回 false。
Soluttion:
有两种实现思路,第一种直接创建长度为行驶最大距离U的数组(实际上创建长度为U+1),利用差分进行累加判定;
class Solution:
def carPooling(self, trips: List[List[int]], capacity: int) -> bool:
d = [0] * 1001
for num, from_, to in trips:
d[from_] += num
d[to] -= num
return all(s <= capacity for s in accumulate(d))
第二种使用平衡树代替差分数组,或者对hash的key进行排序。用排序时间换取降低空间复杂度。
class Solution:
def carPooling(self, trips: List[List[int]], capacity: int) -> bool:
d = Counter()
for num, from_, to in trips:
d[from_] += num
d[to] -= num
s = 0
for k in sorted(d):
s += d[k]
if s > capacity:
return False
return True
二维前缀和
template
class MatrixSum:
def __init__(self, matrix: List[List[int]]):
m, n = len(matrix), len(matrix[0])
s = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(matrix):
for j, x in enumerate(row):
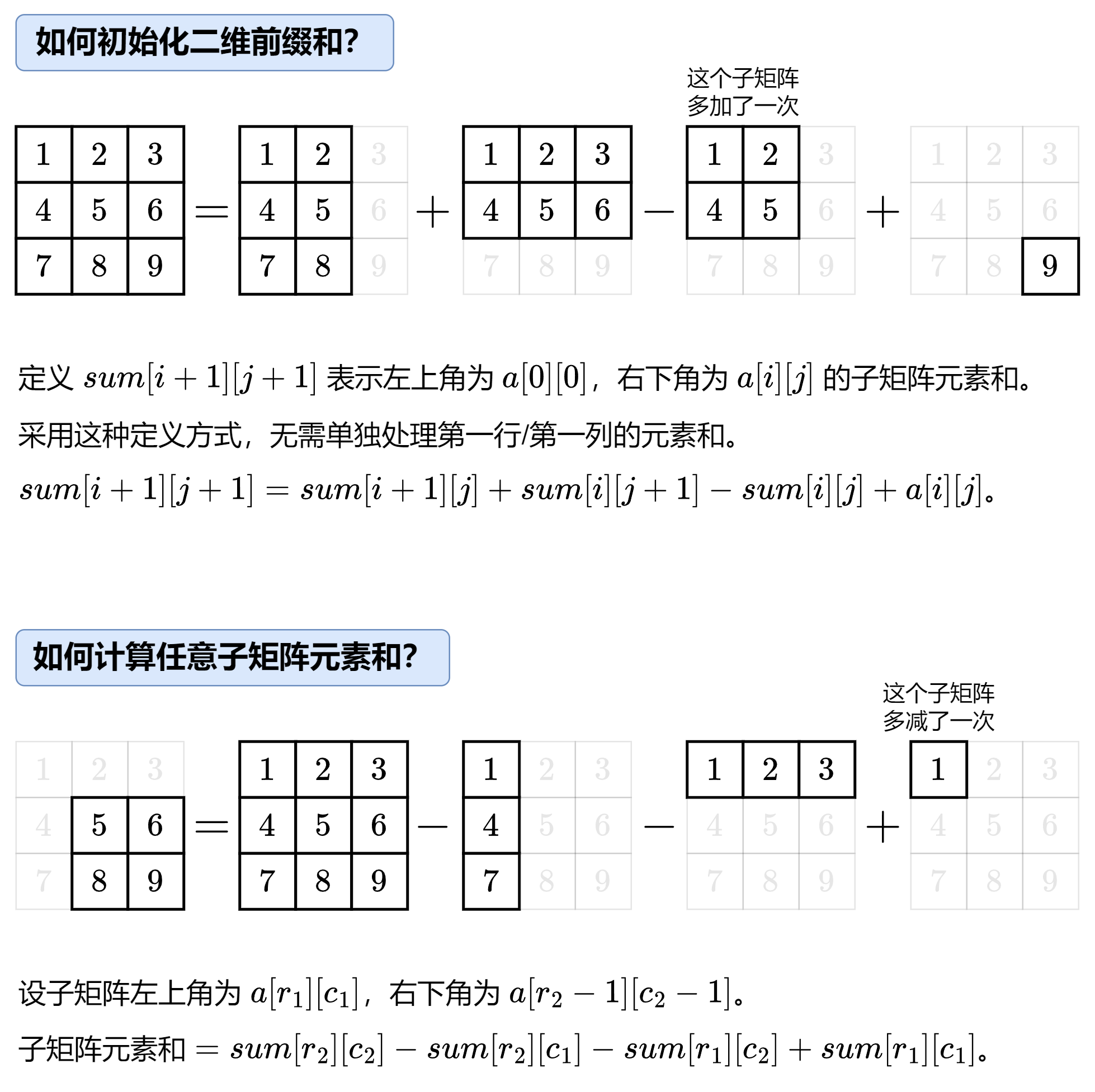
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + x
self.s = s
# 返回左上角在 (r1,c1) 右下角在 (r2-1,c2-1) 的子矩阵元素和(类似前缀和的左闭右开)
def query(self, r1: int, c1: int, r2: int, c2: int) -> int:
return self.s[r2][c2] - self.s[r2][c1] - self.s[r1][c2] + self.s[r1][c1]
# 如果你不习惯左闭右开,也可以这样写
# 返回左上角在 (r1,c1) 右下角在 (r2,c2) 的子矩阵元素和
def query2(self, r1: int, c1: int, r2: int, c2: int) -> int:
return self.s[r2 + 1][c2 + 1] - self.s[r2 + 1][c1] - self.s[r1][c2 + 1] + self.s[r1][c1]
二维差分
Leetcode 题单
差分数组
- 1094. 拼车 ✓
- 航班预订统计
- 将区间分为最少组数
- 字母移位 II
- 使数组中的所有元素都等于零
- 最大化城市的最小供电站数目
二维前缀和
二维差分