[TOC]
Definition
这里红黑树相关定义沿用的是邓公版数据结构中的定义:
-
树高:从根节点到叶节点路径长(空树树高-1,单节点树树高0)
-
红黑树树高:从根节点到外部节点的路径长
Proof
查阅了一圈网上的资料,发现对于红黑树树高的证明只有一个相对较宽松的上界:
设内部节点为n,外部节点为n+1,那么黑高度 bh 满足 bh<=lg(n+1)
故最大高度 h<=2lg(n+1)
但是带入一个例子就可以发现这个上界太高了,比如n=1
所以我们希望找一个真实的最大树高度。
首先我们知道红黑树等价于(2,4)-B树1,那现在其实可以考虑,对于高为h的红黑树,至少有多少个节点。
那将此时节点最少化的红黑树转化为B树之后有两种情况,就是h是否为偶数:
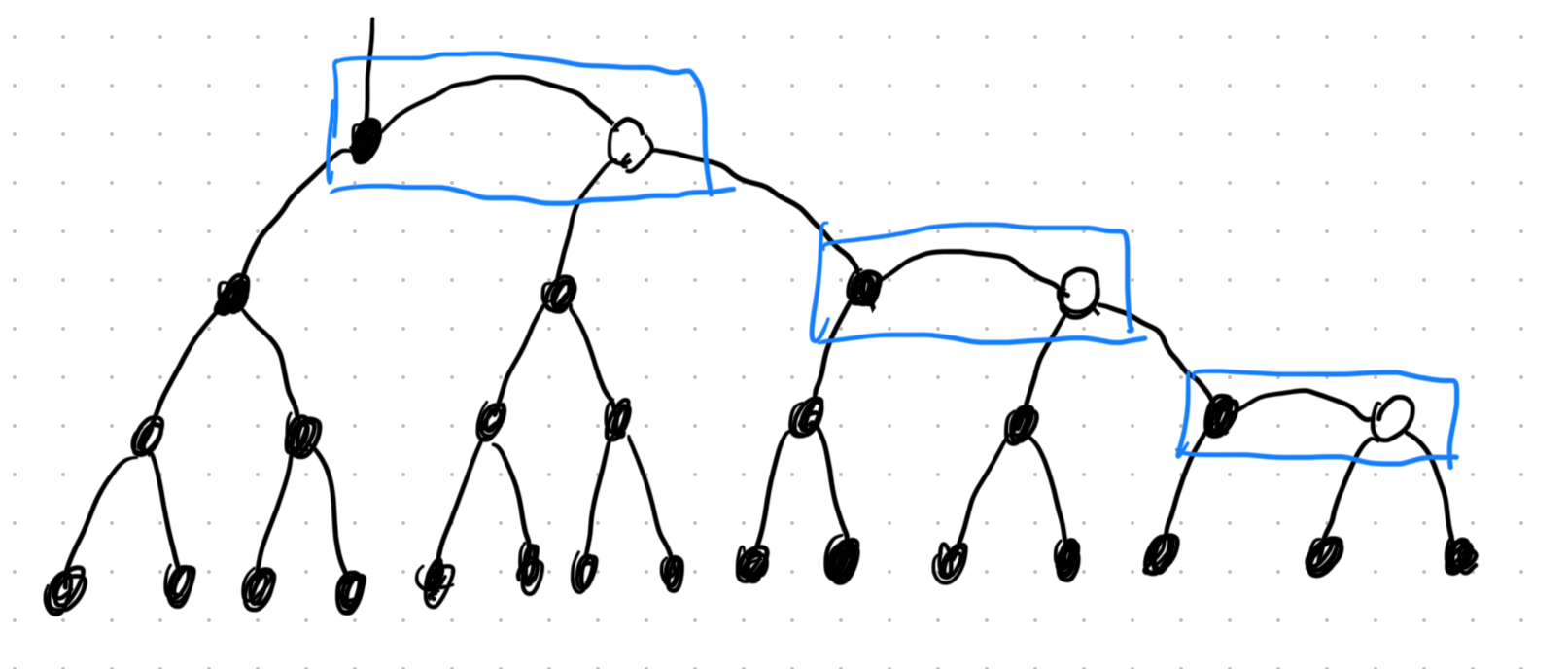
1)h是偶数时,为了能达到树高h至少有一条路径上要增加h/2个红点:
可以计算此时总节点数(内部+外部):
\(N = (2+4+8+...+2^{h/2+1})-1=2^{h/2+2}-3\)
当然也可以转为内部节点表达:
\(n=2^{h/2+1}-2\)
则此时最小树高为:
\(h_{max} = 2*(\lfloor{log_2(n+2)}\rfloor-1)\)
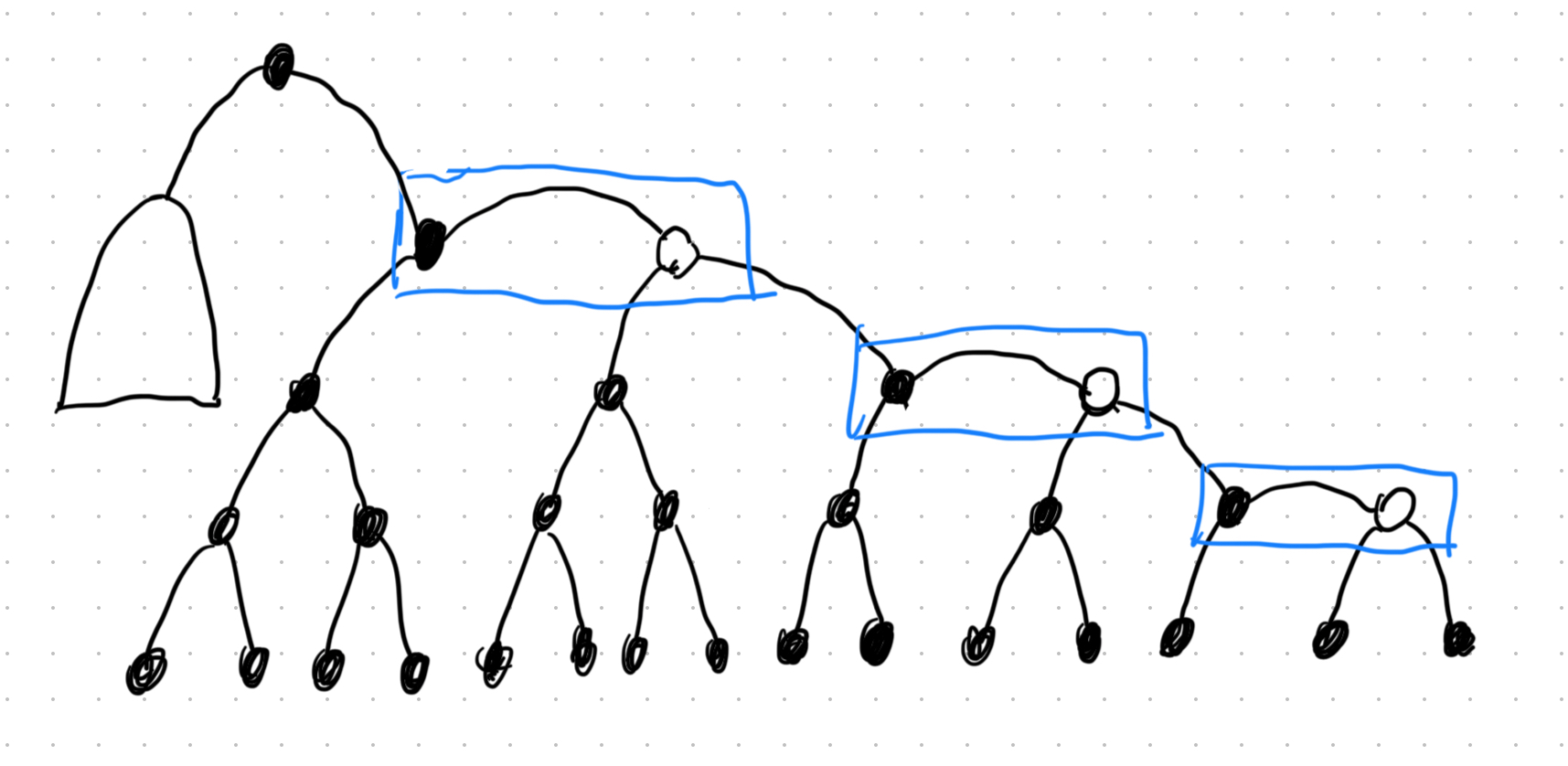
2)h是奇数时,其实就是在根上再接一个黑根,左子树为满黑树(默认最长路径是最右藤)
还是一样,计算此时总节点数(内部+外部):
\(N = (2+4+8+...+2^{(h+1)/2}) + 2^{(h+1)/2} - 1 = 3*2^{(h+1)/2}-3\)
转为内部节点表达:
\(n =3*2^{(h-1)/2}-2\)
则此时最小树高为:
\(h_{max} = 2(\lfloor{log_2((n+2)/3)}\rfloor+1)\)
最终表达式
综上,只需要在两种情况中取最大即是最大树高: \(h_{max} = max(2*(\lfloor{log_2(n+2)}\rfloor-1),2(\lfloor{log_2((n+2)/3)}\rfloor+1))\) 其中 n 为内部节点数。
Reference
-
邓俊辉.数据结构:C++语言版.第2版[M].清华大学出版社,2012. ↩