[TOC]
树状数组1
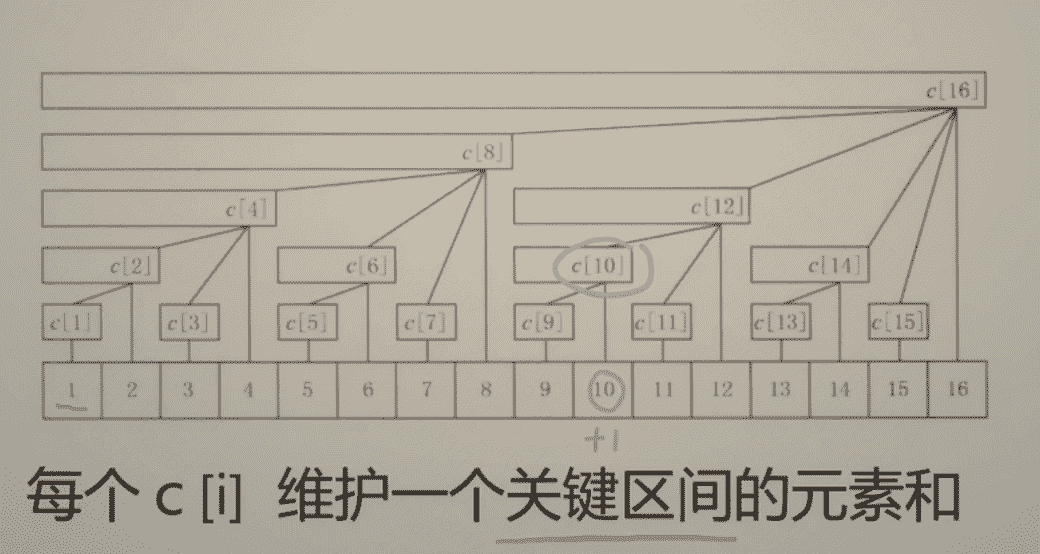
- 初始化O(nlgn): 对每个 nums[i]调用一次 update(i, nums[i])
class NumArray:
__slots__ = 'nums', 'tree'
def __init__(self, nums: List[int]):
n = len(nums)
self.nums = [0] * n # 使 update 中算出的 delta = nums[i]
self.tree = [0] * (n + 1)
for i, x in enumerate(nums):
self.update(i, x)
def update(self, index: int, val: int) -> None:
delta = val - self.nums[index]
self.nums[index] = val
i = index + 1
while i < len(self.tree):
self.tree[i] += delta
i += i & -i
def prefixSum(self, i: int) -> int:
s = 0
while i:
s += self.tree[i]
i &= i - 1 # i -= i & -i 的另一种写法
return s
def sumRange(self, left: int, right: int) -> int:
return self.prefixSum(right + 1) - self.prefixSum(left)
- 初始化O(n): 可以把 update 操作合并到一起。从1 开始枚举 i,把 nums[i−1]加到 tree[i] 后,tree[i] 就算好了,直接把 tree[i] 加到下一个关键区间的元素和中,也就是加到 tree[i+lowbit(i)]中。下下一个关键区间的元素和由 tree[i+lowbit(i)]来更新,我们只需要继续往后枚举 i 即可。
class NumArray:
__slots__ = 'nums', 'tree'
def __init__(self, nums: List[int]):
n = len(nums)
tree = [0] * (n + 1)
for i, x in enumerate(nums, 1): # i 从 1 开始
tree[i] += x
nxt = i + (i & -i) # 下一个关键区间的右端点
if nxt <= n:
tree[nxt] += tree[i]
self.nums = nums
self.tree = tree
def update(self, index: int, val: int) -> None:
delta = val - self.nums[index]
self.nums[index] = val
i = index + 1
while i < len(self.tree):
self.tree[i] += delta
i += i & -i
def prefixSum(self, i: int) -> int:
s = 0
while i:
s += self.tree[i]
i &= i - 1 # i -= i & -i 的另一种写法
return s
def sumRange(self, left: int, right: int) -> int:
return self.prefixSum(right + 1) - self.prefixSum(left)
题单
Reference
-
https://leetcode.cn/problems/range-sum-query-mutable/solutions/2524481/dai-ni-fa-ming-shu-zhuang-shu-zu-fu-shu-lyfll/ ↩