LLM 中的长文本问题

[TOC]

长文本的核心问题

训练端计算、储存分析

以decoder-only为例，一般在训练中考虑的储存为参数、梯度、优化器显存，为4倍参数显存

参数量

self-att: $4h^2+4h$

mlp: $8h^2+5h$

ln: $4h$

embedding: $2vh$ or $vh$ (tied embedding)

梯度、优化器

梯度等于参数量

优化器为参数量2倍

计算量

self-att: $8bsh^2+4bs^2h$

mlp: $16bsh^2$

embedding: $2bshv$

activation

self-att: $11bsh+5bs^2a$

mlp: $19bsh$

ln: $4bsh$

结论是计算量和显存占用都在self-att出现文本长度的2次幂

推理端计算、储存分析

推理端自从有了 KV cache 技术之后，一般思路就是缓存decode步骤中的K、V（activation），牺牲显存使得计算分摊到每一个decode步骤上（注意只是近似分摊），在依然需要$O(s^2)$显存的基础上计算近似接近$O(s)$

***关键瓶颈

这个问题主要是看你从什么方面看

1）从roofline model角度上看：

• 如果是对于transformer，优化瓶颈在于att (flash & flat) 的两个matmuls。为什么呢？因为这部分是memory-bound的：

  • 这部分是activation-activation计算，存在内存(GPU内)切换
  • activation计算涉及softmax这样的操作

  表现就是，即使增大batchsize，也不会缓解。

• 如果是LLM，优化瓶颈是在W_qkv,W_o,FFN$\times$2这些位置 (flashllm)，为什么呢？因为decode阶段的存在，这部分都是瘦矩阵参与计算，用不了tensorcore的并行性

2）从长文本上看：

• 性能上看：主要是计算和储存二次方的问题
• 最近听到一种有趣的说法，说瓶颈是在softmax（即使flash att也不能缓解）

目前的研究方向

训练端

主要bottlenack是显存，有几个思路改进：

• 并行
• 改造attention或优化dataflow
• offload

推理端（sft or infer）

考虑到位置编码失效：

• 位置编码外推

什么是外推？

长度外推性是一个训练和预测的长度不一致的问题：

• 预测的时候用到了没训练过的位置编码（不管绝对还是相对）
• 预测的时候注意力机制所处理的token数量远超训练时的数量。

考虑到显存（KV cache）：

• 优化 attention

训练端优化

• ABF（Adjusted Base Frequency），提高base

• 并行化计算，典型方法如 sequence parallelism
• 优化 attention 机制，典型方法如 Transformer-XL, Longformer
• 引入 memory 机制，典型方法如 Focused Transformer, Memorizing Transformer
• 引入采样机制，典型方法如 Hierarchical transformers, Dynamic-Pooling Transformer

Sequence Parallel

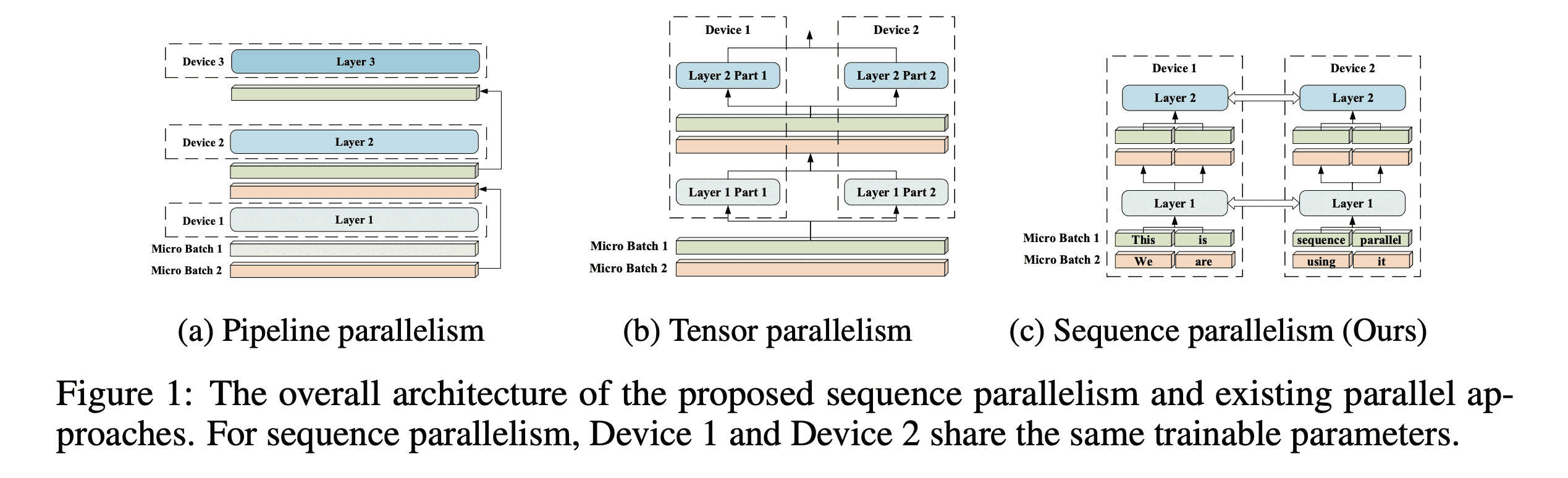
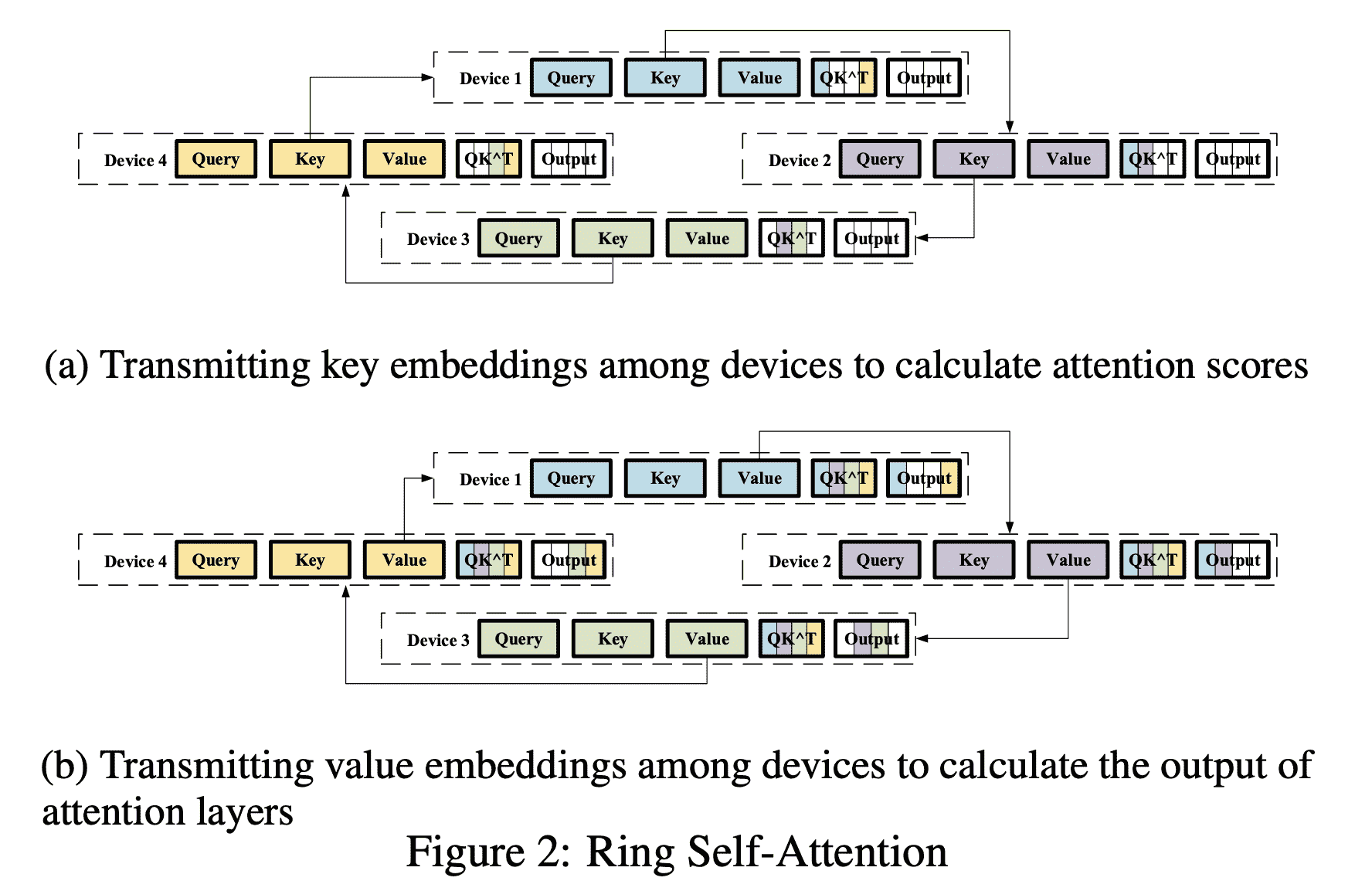
实现这个流程最重要的技术是环状注意力机制：

Focused Transformer

LongLLaMA

长文本在性能上存在 Distraction Issue

Memory Attention Layers 以及 CrossBatch 技术，在 Inference 的过程中，绿色的 Memory Attention Layers 使用 kNN 对外部的 Memory 进行查询，从而有效延长了上下文长度，而 Memory Attention Layers 则主要使用 CrossBatch 进行训练

推理端优化

位置编码外推

典型的位置编码方式有两类：

• 绝对位置编码：即将位置信息融入到输入中
• 相对位置编码：微调Attention结构，使其能够分辨不同位置的Token

绝对位置编码外推

一般来说, 绝对位置编码会加到输入中: 在输入的第 $k$ 个输入向量 $x_k$ 中加入位置向量 $p_k$ 得到 $x_k+p_k$, 其中 $p_k$ 仅依赖于位置 $k$ 。

1）训练式编码

即把位置当做词表一样，训练一个[max_length,hidden_dim]位置向量矩阵。存在一个从n到n^2的外推性[^3]

假设已经训练好的绝对位置编码向量为 $p_1, p_2, \ldots, p_n$, 希望能在此基础上构造一套新的编码向量 $p_1, p_2, \ldots, p_m$, 其中 $m>n$ 。为此, 设 \(\boldsymbol{q}_{(\mathrm{i}-1) \times n+j}=\alpha \boldsymbol{u}_{\mathrm{i}}+(1-\alpha) \boldsymbol{u}_{\mathrm{j}}\)

其中超参 $\alpha \in(0,0.5) \cup(0.5,1), \boldsymbol{u}1, \boldsymbol{u}_2, \ldots, \boldsymbol{u}{\mathrm{n}}$ 是该套位置编码的“基底”。为了保障 $\boldsymbol{q}1=\boldsymbol{p}_1, \boldsymbol{q}_2=\boldsymbol{p}_2, \cdots, \boldsymbol{q}{\mathrm{n}}=\boldsymbol{p}{\mathrm{n}}$, 这样就能反推出各个 $\boldsymbol{u}{\mathrm{i}}:$ \(\boldsymbol{u}_{\mathrm{i}}=\frac{\boldsymbol{p}_{\mathrm{i}}-\alpha \boldsymbol{p}_1}{1-\alpha}, \quad \mathrm{i}=1,2, \cdots, \mathrm{n}\)

这样就最大可以表示出 $n^2$ 个位置的编码。

2）正弦（Sinusoidal）位置编码

这种方案也是Attention Is All You Need 中提出的方法 \(\left\{\begin{array}{l} \boldsymbol{p}_{\mathrm{k}, 2 \mathrm{i}}=\sin \left(\mathrm{k} / 10000^{2 \mathrm{i} / \mathrm{d}}\right) \\ \boldsymbol{p}_{\mathrm{k}, 2 \mathrm{i}+1}=\cos \left(\mathrm{k} / 10000^{2 \mathrm{i} / \mathrm{d}}\right) \end{array}\right.\)

其中 $\boldsymbol{p}{\mathrm{k}, 2 \mathrm{i}}, \boldsymbol{p}{\mathrm{k}, 2 \mathrm{i}+1}$ 分别是位置 $k$ 的编码向量的第 $2 i, 2 i+1$ 个分量, $d$ 是位置向量的维度。

根据以上定义, 我们可以非常简单计算得到Sinusoidal位置编码的值, 并绘制图像研究其规律。整体位置编码如下图所示（纵轴position，横轴hidden_dim）:

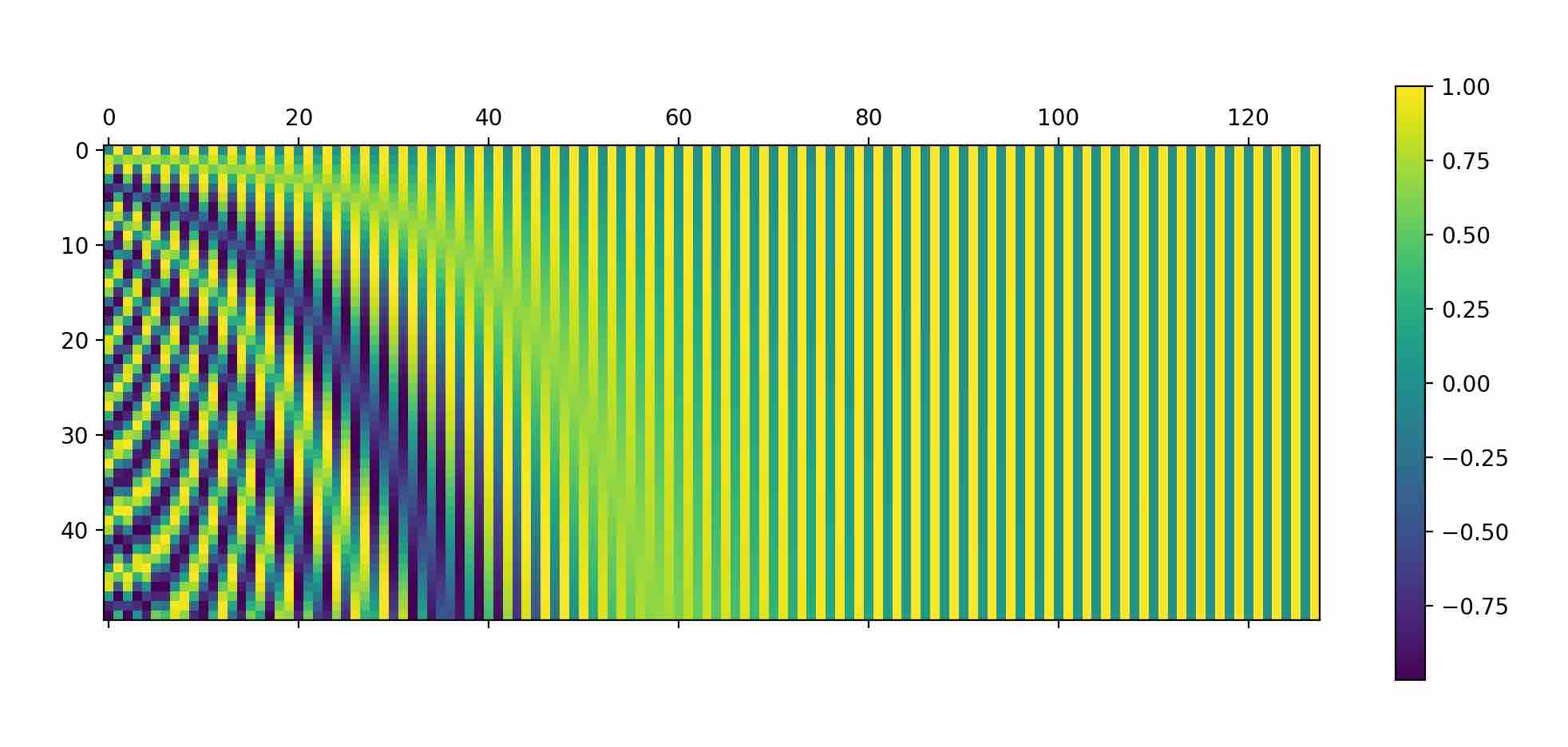
从两个截面上去看：

• position确定的时候，dim越大，频率越低并逐渐收敛；pos越大，启始频率越大；
• dim确定的时候，频率确定；dim越大，频率越小；

问题1: 为什么用包含各频率的正弦和余弦对？

位置编码存储的是一个包含各频率的正弦和余弦对，这样做有两个好处：

• 可以使得不同位置的编码向量之间有一定的规律性，比如相邻位置之间的差异较小，而距离较远的位置之间的差异较大。这是由正弦和余弦函数的连续性和单调性保证的，即对于任意两个相邻的位置，它们对应的编码向量在每一个维度上都只有微小的变化，而对于任意两个距离较远的位置，它们对应的编码向量在每一个维度上都有较大的差异。
• 可以使得编码向量在任意维度上都能保持唯一性，即不同位置在同一个维度上不会有相同的值。这是由正弦和余弦函数的周期性和相位差保证的，即对于任意两个不同的位置，它们对应的编码向量在每一个维度上都不相等。

问题二：底数对结果的影响是什么？

底数越大，位置向量能表示的序列就越长，这是大底数的好处。但是，底数大，意味着在-1到+1的范围内向量的取值越密集，造成两个位置的向量距离越近，这对后续的Self-Attention模块来说是不利的，因为它需要经历更多的训练次数才能准确地找到每个位置的信息，或者说，才能准确地区分不同的位置。长序列需要长编码。但这样又会增加计算量，特别是长编码会影响模型的训练时间。所以，那个底数并非是越大越好。

问题三：Sinusoidal 位置编码如何外推

三角函数式位置编码的特点是有显式的生成规律，因此可以期望于它有一定的外推性。另外一个使用它的理由是：由于 \(\begin{aligned} & \sin (\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta \\ & \cos (\alpha+\beta)=\cos \alpha \cos \beta-\sin \alpha \sin \beta \end{aligned}\)

这表明位置 $\alpha+\beta$ 的向量可以表示成位置 $\alpha$ 和位置 $\beta$ 的向量组合, 这提供了位置拓展的可能性。

相对位置编码外推

相对位置并没有完整建模每个输入的位置信息，而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离，由于自然语言一般更依赖于相对位置，所以相对位置编码通常也有着更好的表现，灵活性也更大。

1）旋转位置编码 RoPE

实际上 RoPE 的诸多思想来源于 Sinusoidal 位置编码，区别在于 Sinusoidal 位置编码采用和 word embedding 相加的形式，RoPE 则采用了矩阵相乘的形式。¹

RoPE采用了刚体运动旋转矩阵的形式, 位置为 $n$ 的 $\mathrm{k}$ 向量的表达式为 \(f(k, n)=R_n k=\left(\begin{array}{cc} \cos n \theta & -\sin n \theta \\ \sin n \theta & \cos n \theta \end{array}\right)\left(\begin{array}{l} k_0 \\ k_1 \end{array}\right)\)

可以证明旋转前的 attention 值与旋转后的 attention 值的差值仅与相对位置有关： \(\begin{aligned} & q_m \cdot k_n=f(q, m) \cdot f(k, n)=\left(R_m q\right)^T *\left(R_n k\right)=q^T R_m^T * R_n k \\ & =q^T\left[\begin{array}{cc} \cos m \theta & -\sin m \theta \\ \sin m \theta & \cos m \theta \end{array}\right]^T *\left[\begin{array}{cc} \cos n \theta & -\sin n \theta \\ \sin n \theta & \cos n \theta \end{array}\right] k \\ & =q^T\left[\begin{array}{cc} \cos m \theta & \sin m \theta \\ -\sin m \theta & \cos m \theta \end{array}\right] *\left[\begin{array}{cc} \cos n \theta & -\sin n \theta \\ \sin n \theta & \cos n \theta \end{array}\right] k \\ & =q^T\left[\begin{array}{cc} \cos n \theta \cos m \theta+\sin n \theta \sin m \theta & \sin m \theta \cos n \theta-\sin n \theta \cos m \theta \\ \sin n \theta \cos m \theta-\sin m \theta \cos n \theta & \cos n \theta \cos m \theta+\sin n \theta \sin m \theta \end{array}\right] k \\ & =q^T\left[\begin{array}{cc} \cos (n-m) \theta & -\sin (n-m) \theta \\ \sin (n-m) \theta & \cos (n-m) \theta \end{array}\right] k \\ & =q^T R_{n-m} k \end{aligned}\)

这表明，两个相对位置一定的词embedding，无论绝对位置处在何处，其att是不变的。

以下讨论RoPE的外推法

插值法

一旦我们在模型中有效地整合了相对位置信息, 增加 LLM 上下文窗口的最直接方法就是通过位置插值 (position interpolation, PI) 进行微调。

这种方法实现很简单, 如果希望将预训练阶段的位置向量范围 $[0,2048]$ 外推到 $[0,4096]$, 只需要将对应位置缩放到原先支持的区间 $([0,2048])$ 内：计算公式如下，L为原先支持的长度(如2048), $L^{\prime}$ 为需要扩展的长度(如4096): \(f^{\prime}(x, m)=f\left(x, \frac{m L}{L^{\prime}}\right)\)

其过程如下图所示，本质上缩小旋转角度：


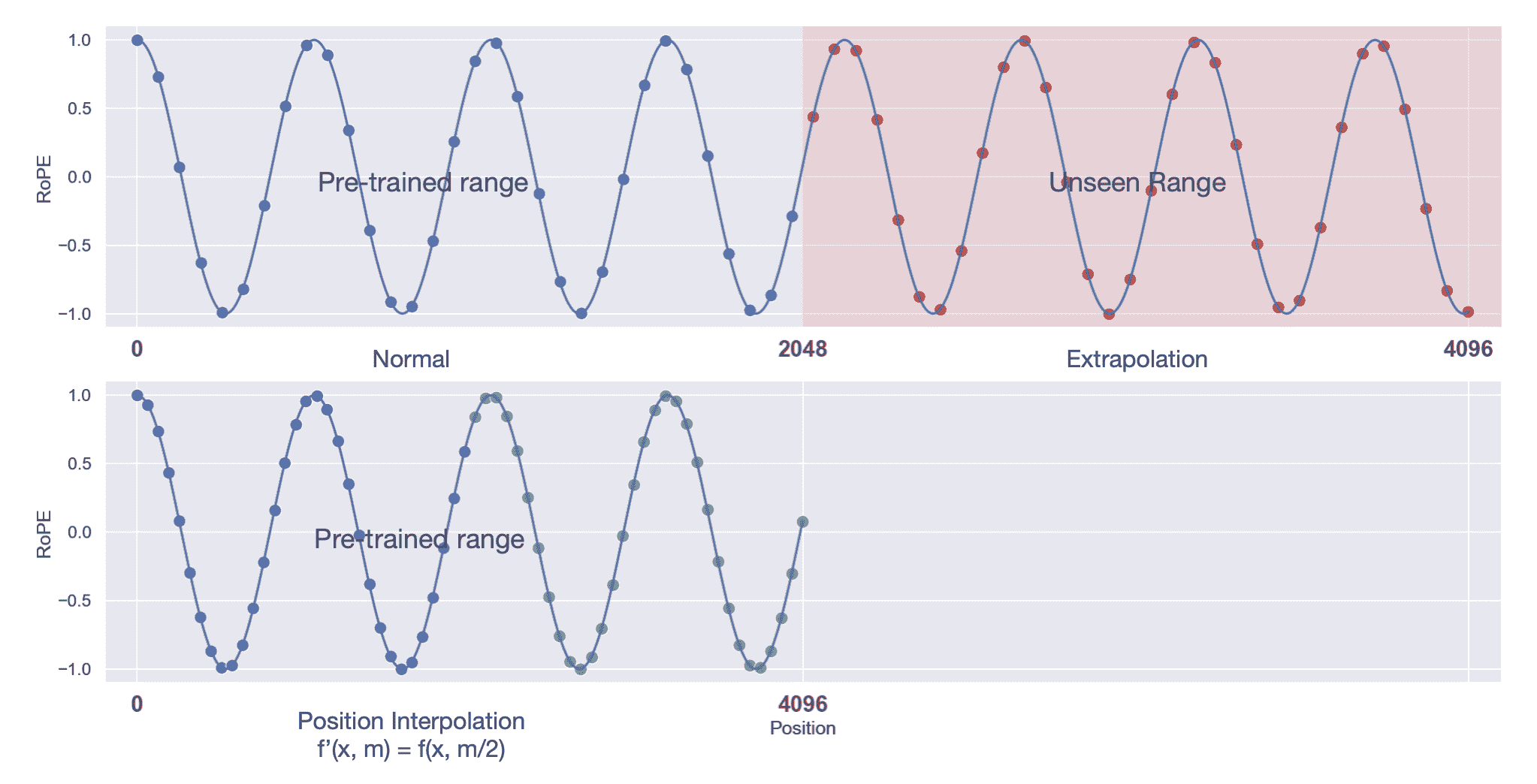
fig refering to ¹

NTK-aware (Neural Tangent Kernel)

这种方式把旋转角修改为 $m *(\text { base } * \alpha)^{-2 \mathrm{i} / \mathrm{d}}$, 其中 $\alpha$ 表示 base 的缩放因子。其修改的方式如上图所示 (横轴为维度, 纵轴为旋转角), 在不同维度上修改的程度不同。这种方式保留了高频信息：

• 高频分量旋转速度降幅低，低频分量旋转速度降幅高；
• 在高频部分进行外推，低频部分进行内插。

这是因为靠前的维度, 在训练中见过非常多完整的旋转周期, 位置信息得到了充分的训练, 所以具有较强的外推能力。靠后的维度, 在训练中无法见到完整的旋转周期, 或者见到的旋转周期非常少, 训练不够充分, 外推性能弱, 需要进行位置插值。

NTK-by-parts

不改变高频部分，仅缩小低频部分的旋转弧度。

Dynamic NTK

这是是一种动态插值的方法：当推理长度小于等于训练长度时，不进行插值；推理长度大于训练长度时，每一步都通过NTK-Aware Interpolation动态放大base。

NTK example

NTK代码如下：

class XverseRotaryEmbedding(torch.nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=500000, device=None):
        super().__init__()
        self.base = base
        self.dim = dim
        self.max_position_embeddings = max_position_embeddings
        inv_freq = 1.0 / \
            (base ** (torch.arange(0, dim, 2).float().to(device) / dim))
        self.register_buffer("inv_freq", inv_freq)

        # Build here to make `torch.jit.trace` work.
        self.max_seq_len_cached = max_position_embeddings

        t = torch.arange(self.max_seq_len_cached,
                         device=self.inv_freq.device, dtype=self.inv_freq.dtype)
        freqs = torch.einsum("i,j->ij", t, self.inv_freq)
        # Different from paper, but it uses a different permutation in order to obtain the same calculation
        emb = torch.cat((freqs, freqs), dim=-1)
        self.register_buffer("cos_cached", emb.cos()[
                             None, None, :, :], persistent=False)
        self.register_buffer("sin_cached", emb.sin()[
                             None, None, :, :], persistent=False)

    def forward(self, x, seq_len=None):
        # x: [bs, num_attention_heads, seq_len, head_size]
        # This `if` block is unlikely to be run after we build sin/cos in `__init__`. Keep the logic here just in case.
        if seq_len > self.max_seq_len_cached:

            t = torch.arange(seq_len, device=x.device, dtype=torch.float32)
            dim = self.dim
            alpha = (seq_len / (self.max_position_embeddings/2) - 1)
            base = self.base * alpha ** (dim / (dim-2))
            ntk_inv_freq = 1.0 / \
                (base ** (torch.arange(0, dim, 2).float().to(x.device) / dim))

            freqs = torch.einsum("i,j->ij", t, ntk_inv_freq)
            emb = torch.cat((freqs, freqs), dim=-1).to(x.device)
            cos_cached = emb.cos()[None, None, :, :]
            sin_cached = emb.sin()[None, None, :, :]
            return (
                cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
                sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype)
            )

        return (
            self.cos_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
            self.sin_cached[:, :, :seq_len, ...].to(dtype=x.dtype),
        )

另一部分问题是如何构建长文本sft数据：以构建多文档QA类数据为例：首先，基于65B模型生成与单个文章有关的高质量问题回答对；然后将文章内容混合成目标长度的整段内容，随机选择与其中某个内容匹配的问题回答对；最后将该问题和回答作为整段内容的问题和回答，构成训练的单个样本。通过上述批量化数据生产管线，我们可以得到32K、64K，一直到256K长度的高质量对话数据。²

YaRN³

YaRN本质上是NTK-by-parts Interpolation与注意力分布修正策略的结合，仅缩小低频部分的旋转弧度，且通过降更低温度系数修正更长文注意力分布。

问题1: base怎么选？

RoPE 中 base 的放大和缩小都能获得很好的外推效果(base=10K 效果最差)。原因在于：

• 当 base 较小时(如 500)，RoPE 的三角函数周期变短，训练时就可以见过完整的 cos/sin 值域；
• 当 base 较大时(如 1000000)，RoPE 的三角函数周期变长，训练时虽然不能见过完整的 cos/sin 值域，但是外推时仍处于单调区间。

2）其他形式的编码方式及其外推

最为出名的T5，ALiBi位置编码，在attention上加权；

其实本质上RoPE也是做这个事情，但是ALiBi是训练前更改，NTK是推理修改；

Attention机制及dataflow优化

做的事情都是注意力稀疏化，为了缓解$O(s^2)$的显存(primary issue)和计算。

类似attention sinks⁴

长文本评估

PPL

$P P L=e^H \text { 其中 } \mathrm{H} \text { 是平均交叉熵} $

$H=-\frac{1}{N} \sum_{i=1}^N \log 2\left(P\left(w_i \mid w_1, w_2, \ldots, w{i-1}\right)\right)$

PPL的问题¹：

• 模型词汇量可能会不公平地影响PPL：PPL 在很大程度上依赖于模型的词汇量及其概括未见过的单词的能力。如果模型遇到训练数据中不存在的单词或短语，即使生成的文本有意义，其 PPL 分数也较高。
• 缺乏主观性考虑：PPL 是一种客观指标，不考虑主观因素，例如风格、创造力或特定环境下的适当性。
• 上下文理解：PPL 主要关注于根据前面的上下文预测下一个单词。然而，它可能无法捕捉模型对更广泛背景的整体理解。
• 语言歧义和创造力：PPL 并不能体现模型处理语言歧义或生成创造性和新颖输出的能力。
• 领域特异性：PPL 对训练数据的领域和分布很敏感。在特定领域训练的模型可能会在其领域内实现较低的复杂性，但可能需要帮助在其训练环境之外生成文本。
• 过度拟合和泛化：PPL可能会受到过度拟合的影响，其中模型在训练数据上表现得非常好，但很难泛化到看不见的或现实世界的例子。

StreamingLLM 就很好地证明了 PPL 的局限性，因为尽管 StreamingLLM 的 PPL 值较低，但是由于其损失了大量中间信息，因此无法在“大海捞针”等测试方法中有较好的表现。¹

“大海捞针”

“大海捞针” 由 Greg Kamradt 提出的大模型长文本性能测试方法，其做法是在文本语料中藏入一个与文本语料不相关的句子，然后看大模型能不能通过自然语言提问的方式（Prompt）把这句话准确地提取出来。Greg Kamradt 的“大海捞针”实验简述：

“大海”：Paul Graham 的文章合集作为语料 “针”：“The best thing to do in San Francisco is eat a sandwich and sit in Dolores Park on a sunny day.” 提问：”What is the most fun thing to do in San Francisco based on my context? Don’t give information outside the document” 期待模型输出的正确答案： The best thing to do in San Francisco is eat a sandwich and sit in Dolores Park on a sunny day.

• GPT-4 Turbo（128K）在语料长度超过 72K 且句子（“针”）藏在文本头部的时候，准确率不佳。
• Claude 2.1似乎在语料长度超过20K之后就开始准确率不佳，而且句子（“针”）藏在语料靠前的位置时，准确率尤其差。
• Kimi 和 Qwen-72B-chat 表现挺好。

Reference

• Previous
  携程2025届算法笔试
• Next
  RLHF Cookbook