[TOC]
PPO(Proximal Policy Optimization)
PG(Policy Gradient)
假设R(eword)函数遵循马尔可夫链,求R对$\theta$ (决策的神经网络) 的导数: \(\begin{gathered}\nabla \bar{R}_\theta=\frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} R\left(\tau^n\right) \nabla \log p_\theta\left(a_t^n \mid s_t^n\right) \\ =\frac{1}{N} \sum_{n=1}^N R\left(\tau^n\right)\left[\sum_{t=1}^{T_n} \nabla \log p_\theta\left(a_t^n \mid s_t^n\right)\right]\end{gathered}\) 这样就可以执行PG (Policy Gradient)
Importance Sampling(重要性采样)
对于一个服从概率p分布的变量x, 我们要估计f(x) 的期望。直接想到的是,我们采用一个服从p的随机产生器,直接产生若干个变量x的采样,然后计算他们的函数值f(x),最后求均值就得到结果。但这里有一个问题是,对于每一个给定点x,我们知道其发生的概率,但是我们并不知道p的分布,也就无法构建这个随机数发生器。因此需要转换思路:从一个已知的分布q中进行采样。通过对采样点的概率进行比较,确定这个采样点的重要性。
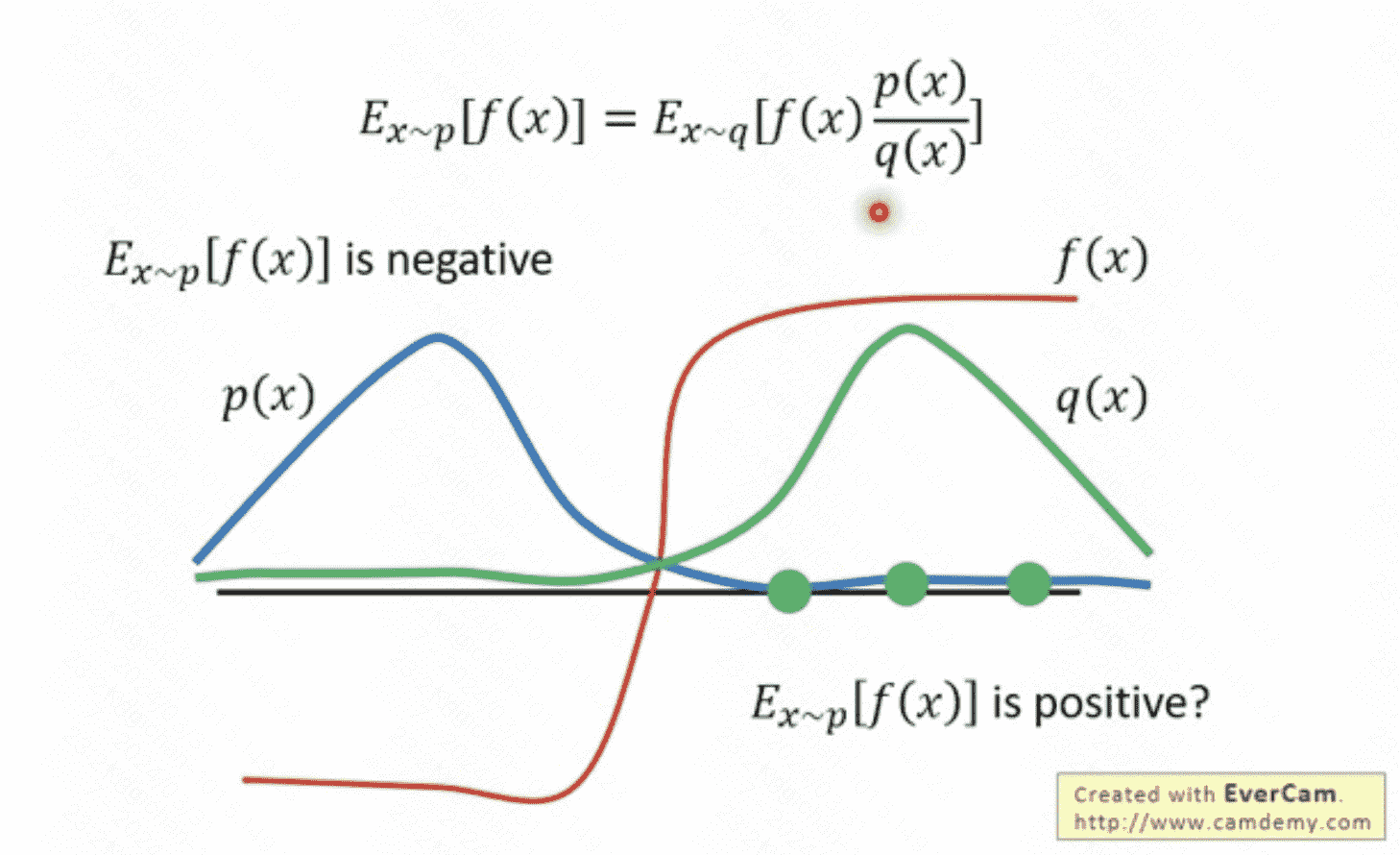
上图说明p分布和q分布差距不能过大,否则,会由于采样的偏离带来谬误。
PPO
PPO来自于PG的几个改进点:
-
折扣因子:未来预期reward需要加权,因为未来不如现在重要。
-
baseline/优势函数/cratical model:PG可能每步都是有正reward的,如果我们减去一个baseline reward,就可以出现正负reward,有利于模型优化;Furthermore,如果我们训练一个critical model来生成未来的预期的折扣reward,就可以更细致地更新baseline。
-
From on-policy to off-policy:按PG的策略,没更新一次参数$\theta$,需要重新进行策略采样,但是这样效率低下,因此需要换为off-policy的策略,通过另一套参数的采样更新自己,那偏差怎么解决,就用重要性采样: \(\nabla \bar{R}_\theta=E_{\tau \sim p_{\theta^{\prime}}(\tau)}\left[\frac{p_\theta(\tau)}{p_{\theta^{\prime}}(\tau)} R(\tau) \nabla \log p_\theta(\tau)\right]\)
- Sample the data from $\theta^{\prime}$.
- Use the data to train $\theta$ many times.
加上优势函数的最终公式为: \(\nabla \bar{R}=\sum_{t=1}^T \frac{p_\theta\left(a_t \mid s_t\right)}{p_{\theta^{\prime}}\left(a_t \mid s_t\right)} A_t\left(s_t, a_t\right)-\lambda K L\left[\theta, \theta^{\prime}\right]\)
其中优势函数为: \(A^\theta\left(s_t, a_t\right)=\sum_{t^{\prime}>t} \gamma^{t^{\prime}-t} r_{t^{\prime}}-V_\phi\left(s_t\right)\) 这里加上了KL散度惩罚项,防止采样偏差过大。
PPO需要更新的参数:
一套策略参数$\theta$,他与环境交互收集批量数据,然后批量数据关联到 的副本中。他每次都会被更新。
一套策略参数的副本$\theta’$ ,他是策略参数与环境互动后收集的数据的关联参数,相当于重要性采样中的q分布。
一套critic网络的参数$\phi$,他是基于收集到的数据,用监督学习的方式来更新对状态的评估。他也是每次都更新。
PPO算法伪代码

DPO(Direct Preference Optimization)
DPO作为利用人类preference数据直接训练模型的方法,跳过了Reward Model和强化学习部分的训练,Mixtral也用了DPO去训练模型。1
KL Divergence
Kullback–Leibler divergence用于度量两个概率分布之间的距离,衡量两个概率分布的相似程度。当然严格来说KL divergence不是一种度量(metric),因为它不满足对称性,具体的数学性质可参考Wiki[3]。KL divergence定义如下: \(D_{\mathrm{KL}}(P \| Q)=\sum_{x \in \mathcal{X}} P(x) \log \left(\frac{P(x)}{Q(x)}\right)\) which is equivalent to \(D_{\mathrm{KL}}(P \| Q)=-\sum_{x \in \mathcal{X}} P(x) \log \left(\frac{Q(x)}{P(x)}\right) \\ D_{\mathrm{KL}}\ge 0,等号成立当且仅当 P、Q一致\) KL divergence经常被用来设计Auxiliary Loss以约束一些复杂的概率分布,使其具备某些想要的性质。比如在AutoEncoder中,用它来约束Latent Space,使其接近一个简单的高斯分布。在RLHF训练范式中,我们用它来约束新的语言模型,使其尽可能和预训练语言模型的概率分布保持一致,防止其过拟合于Reward Model(RM)1。
Bradley–Terry model
Bradley–Terry model被用于对事物间的比较关系进行建模。 \(P(i>j)=\frac{e^{\beta_i}}{e^{\beta_i}+e^{\beta_j}}\)
DPO objective
根据损失函数(最大reward+KL(model, ref_model))的最大似然估计,可以得到: \(p^*\left(y_1 \succ y_2 \mid x\right)=\frac{1}{1+\exp \left(\beta \log \frac{\pi^*\left(y_2 \mid x\right)}{\pi_{\mathrm{ref}}\left(y_2 \mid x\right)}-\beta \log \frac{\pi^*\left(y_1 \mid x\right)}{\pi_{\mathrm{ref}}\left(y_1 \mid x\right)}\right)}\)
然后我们可以发现, 由于这个模型计算概率的时候只关心两个样本reward的差值, 因此这里的 $\log Z(x)$ 项被抵消了! 于是我们可以转而用MLE直接在这个概率模型上直接优化LM, 去得到我们希望的最优的 $\pi^*$ 。 \(\mathcal{L}_{\mathrm{DPO}}\left(\pi_\theta ; \pi_{\text {ref }}\right)=-\mathbb{E}_{\left(x, y_w, y_l\right) \sim \mathcal{D}}\left[\log \sigma\left(\beta \log \frac{\pi_\theta\left(y_w \mid x\right)}{\pi_{\text {ref }}\left(y_w \mid x\right)}-\beta \log \frac{\pi_\theta\left(y_l \mid x\right)}{\pi_{\text {ref }}\left(y_l \mid x\right)}\right)\right]\)
以上就是DPO的训练目标,其实依然是Bradley-Terry model的MLE。
改进训练方法
在实际当中,DPO一般通过两步骤进行训练:
- 首先用ref model生成样本对,由人类进行标注,得到人类偏好数据;
- 在人类偏好数据上优化模型,目标就是上述的DPO训练目标。
但一般来说由人类去标注数据成本很高,而我们更容易去获得开源的偏好数据,所以步骤会调整为:
- 用收集的人类偏好数据中更受偏好的数据SFT模型;
- 在该SFT模型上,用人类偏好数据,通过DPO训练目标训练模型。
第一步的目的是让模型的生成数据分布尽可能和标注数据一致。
Reference
-
Fine-tune Llama 2 with DPO:Fine-tune Llama 2 with DPO ↩ ↩2