[TOC]
Abstract
达到的效果:bounded memory and computation
方法的本质:new attention technique dubbed Infini-attention, 即修改的attention机制
Intro
宏观的想法上就是Q分别在 previous segments 和 local segmenet上分别做attention,只对后者施加casual mask。但是乍一看这个实现的复杂度还是O(n^2),因为KV cache策略就是这样做的。

Infini-ATT
在具体实现上,模仿RNN构建了一个循环的hidden_states,用以总结上文的信息:
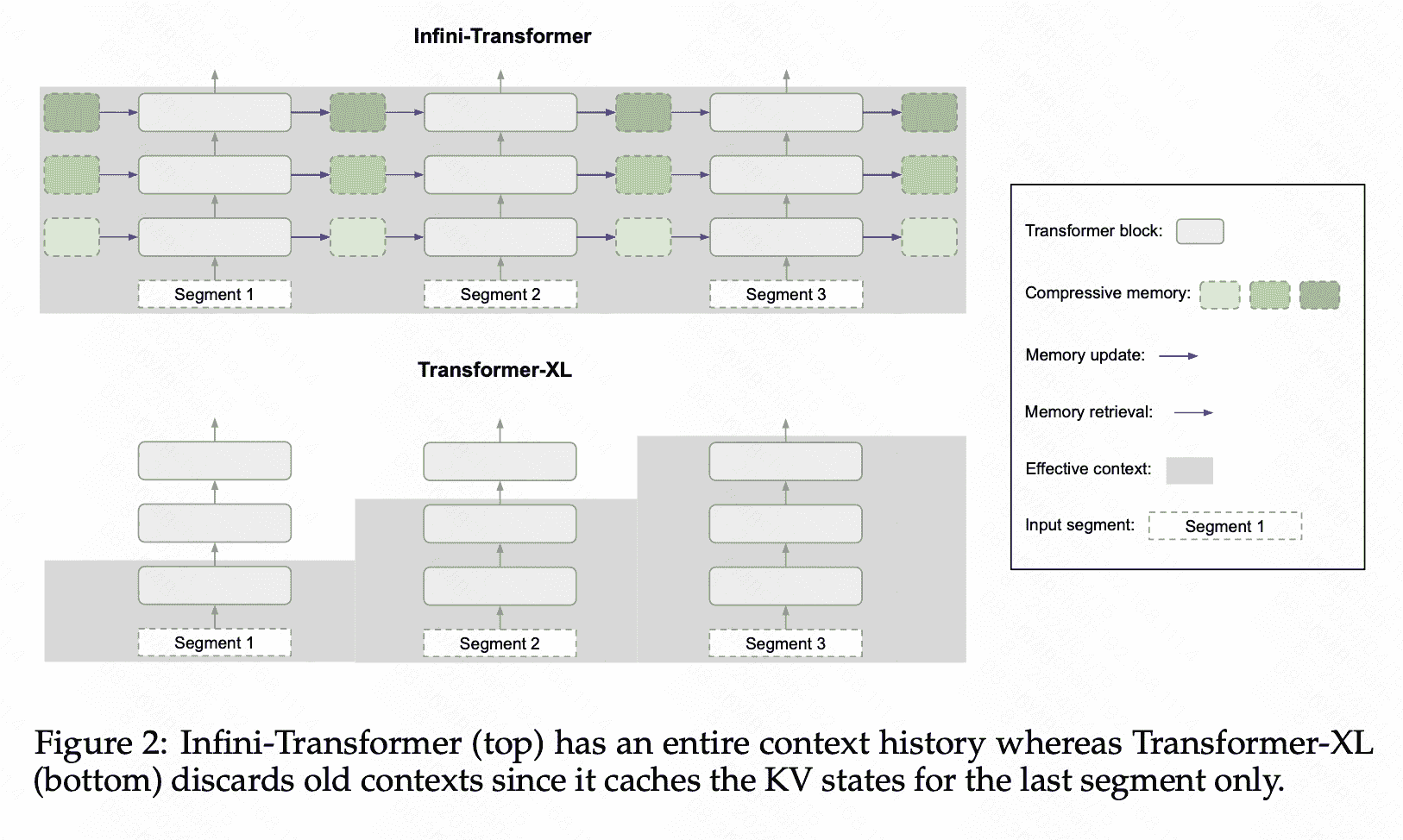
memory retrieval
首先从最基础的attention出发: \(A_i=softmax(Q_iK^T)V=\frac{\Sigma_{j=1}^isim(Q_iK^T_j)V_j}{\Sigma_{j=1}^isim(Q_iK^T_j)}\) 其中, \(sim(q,k)=\frac{exp(qk^T)}{\sqrt{dim}}\) 之后为了使得推导进行下去,infini-att用了一个特殊的activation function:use element-wise ELU + 1 as the activation function (e.g. $\phi(x)=elu(x)+1$),这个af可以进行乘积分解: \(A_i=\frac{\Sigma_{j=1}^i\phi(Q_i)\phi(K^T_j)V_j}{\Sigma_{j=1}^i\phi(Q_i)\phi(K^T_j)}=\frac{\phi(Q_i)\Sigma_{j=1}^i\phi(K^T_j)V_j}{\phi(Q_i)\Sigma_{j=1}^i\phi(K^T_j)}=\frac{\sigma(Q_i)M_{i-1}}{\sigma(Q_i)z_{i-1}}\)
Memory update
- Linear
由上面的推导可以得到更新规则: \(M_s \leftarrow M_{s-1}+\sigma(K)^T V \text { and } z_s \leftarrow z_{s-1}+\sum_{t=1}^N \sigma\left(K_t\right)\)
- Linear+Delta
应用增量进行更新: \(M_s \leftarrow M_{s-1}+\sigma(K)^T\left(V-\frac{\sigma(K) M_{s-1}}{\sigma(K) z_{s-1}}\right)\) 原理就是用当前V减去隐藏V,其实就是V在之前K上的加权平均: \(\frac{\sigma(K) M_{s-1}}{\sigma(K) z_{s-1}}=\frac{\phi(K_i)\Sigma_{j=1}^i\phi(K^T_j)V_j}{\phi(K_i)\Sigma_{j=1}^i\phi(K^T_j)}\)
Long-term context injection
每一个层,每一个头学习一个标量用来混合local注意力、retrieval memory:We aggregate the local attention state $A_{\text {dot }}$ and memory retrieved content $A_{\text {mem }}$ via a learned gating scalar $\beta$ : \(A=\operatorname{sigmoid}(\beta) \odot A_{\text {mem }}+(1-\operatorname{sigmoid}(\beta)) \odot A_{\text {dot }} .\) 最终的输出为: \(O=\left[A^1 ; \ldots A^H\right] W_O\)
Exp
由于Attention机制是重新设计的,所以infini-att不仅仅在系统层面,因此需要重新训练&准确率评估。
一个Gating score visualization,可以看出不同头对上文的注意力不同:

实验主要包括:
1)大海捞针
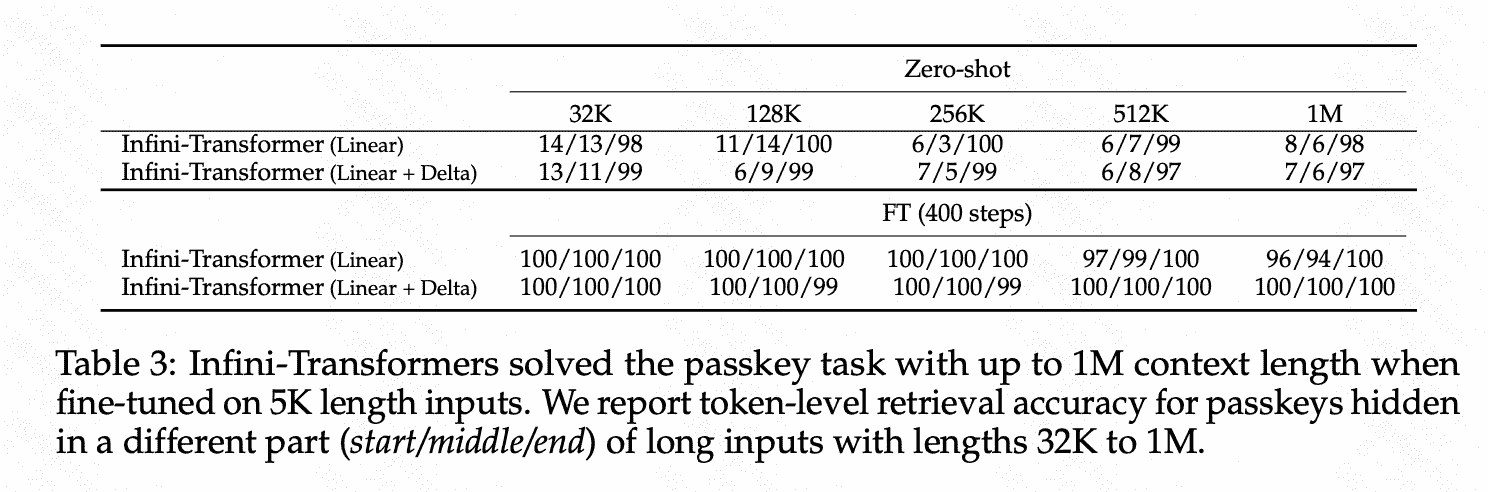
2)summarization