优化器Optimizer从0到1

[TOC]

SGD

Naive SGD

梯度下降法中，每一个step需要在全部数据集上计算Loss之后再用反向传播得到所有参数的梯度。这种方式的坏处是如果数据量很大的话，计算量很大，这让训练数据不容易规模化。

随机梯度下降法 SGD（Stochastic Gradient Descent，SGD）每次随机挑一个 mini-batch 数据来优化神经网络的参数。这种方式可以近似地等价于原始的梯度下降法。优点：保证精度的同时降低计算量，让神经网络可以应用于更大规模的数据上。

我们将SGD算法用公式表示为: $\theta_{t+1}=\theta_t-\gamma g_t$

其中 $\theta, \gamma, g$ 分别代表参数、学习率和梯度。

Momentum SGD

在使用SGD算法时，我们有时会遇到震荡的问题，导致模型收敛过慢。如下图所示：

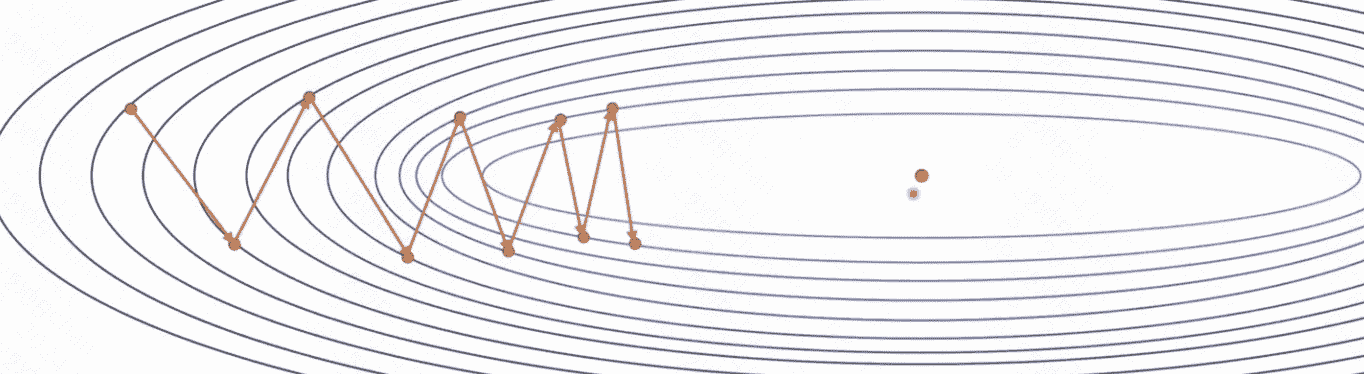
截屏2024-04-20 09.22.09

这种现象是由于每次迭代后梯度变化过大导致的，而解决这个问题的方法就是引入动量（Momentum）的概念。

引入动量的好处是可以抵消梯度中那些变化剧烈的分量，如下图所示，如果我们每次都叠加历史梯度，那么它纵向上变化剧烈的梯度就可以被抵消，从而加快收敛速度：

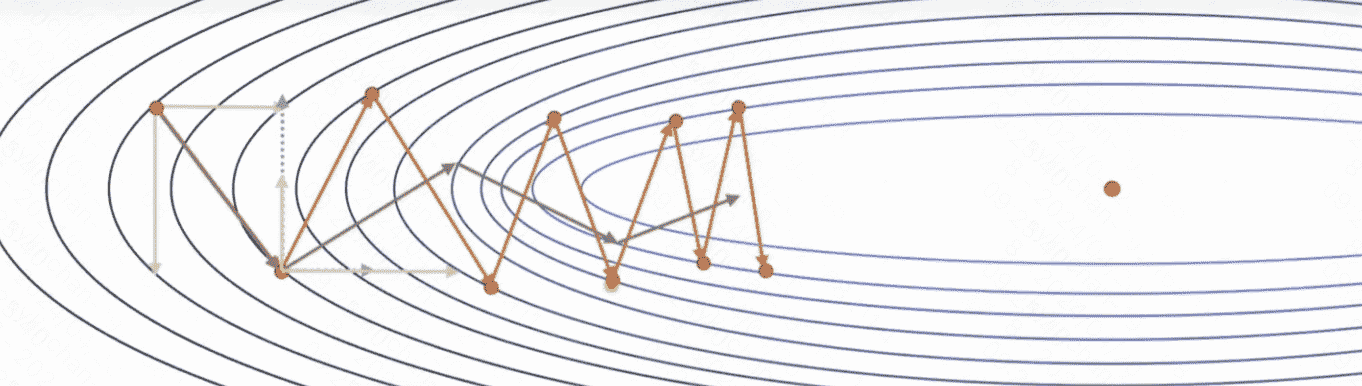
截屏2024-04-20 09.23.43

加入动量之后的SGD算法的公式为: $\theta_{t+1}=\theta_t-\gamma v_t$

其中, $v_t=\mu v_{t-1}+g_t$ 代表当前时刻的梯度； $\mu$ 参数用于指数加权移动平均, 该方法可以减小更早时刻梯度对当前梯度的影响, 通常 $\mu$ 取值为 0.9 。

NAG

Momentum有一个问题就是动量累积的问题，导致更新速度越来越快，造成在最优点处震荡。

NAG(Nesterov’s Accelerated Gradient)算法就是为了解决这个问题而提出的，它的基本原理是在梯度更新之前往前看一步，让优化器可以预知未来的情况，从而对现在的梯度进行调整。

NAG的公式为： $\theta_{t+1}=\theta_t-\gamma v_t$

其中, $v_t=\mu v_{t-1}+g\left(\theta_t-\mu v_{t-1}\right)$, 这里的 $g\left(\theta_t-\mu v_{t-1}\right)$ 就是根据当前梯度方向向前走一步之后再计算出来的梯度。通过这种方式, 在接近最优解时, Nesterov优化器比标准动量SGD算法有更快的收玫速度。因为这种“前瞻性”的操作能帮助优化器避免走得太远, 就像是提前刹车, 所以在接近最优解时更加稳定。

SGD in pytorch

Pytorch 中SGD的算法说明¹：

截屏2024-04-20 09.37.17

这里存在一个问题，就是NAG的实现和上面讲的看起来不一致，根据²的解释：

NAG的另一种定义（本质是学习率是不是提出来）：

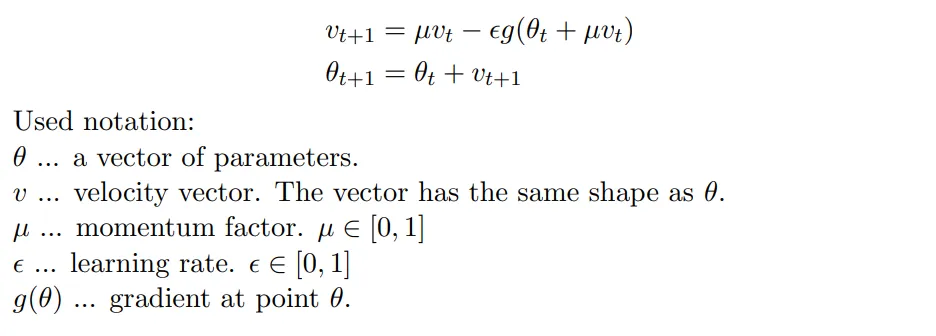
v2-b627cc61574abf0e3648e4ef634c9803_1440w

如果我们每次都按照原始的公式去计算未来点的梯度，可能会造成计算量过大的问题，所以我们要对它进行简化。简化时，我们可以认为当前的位置就已经站在“未来点”（shifted point）上了，然后我们根据Nesterov算法去预测下一个“未来点”，公式推导如下：

v2-909ab130dfdf2abb4d627225a3f0648b_1440w

第二步推导注解³： $\begin{aligned} \theta_{t+1}^{\prime} & =\underbrace{\theta_{t+1}}+\mu V_{t+1} \\ & =(\underbrace{\theta_t}+V_{t+1})+\mu V_{t+1} \\ & =(\theta_{t}^{\prime}-\underbrace{\mu V_t})+V_{t+1}+\mu V_{t+1} \\ & =\theta_t^{\prime}-(V_{t+1}+\varepsilon g\left(\theta_t^{\prime}\right))+V_{t+1}+\mu V_{t+1} \\ & =\theta_t^{\prime}-\varepsilon g\left(\theta_t^{\prime}\right)+\mu V_{t+1} \end{aligned}$

AdaGrad（Adaptive Gradient）

SGD使用统一的学习率更新策略，有附加的学习率更新方法：

余弦退火：

余弦退火是一种学习率调度策略，它根据余弦函数的周期性特性来调整学习率。在每个周期内，学习率从初始值逐渐减小到最小值，然后再逐渐增加到初始值。这个过程不断重复，形成多个周期。

具体来说，在第t个批次（batch），学习率计算公式如下： $lr_t = lr_{min} + 0.5 * (lr_{max} - lr_{min}) * (1 + cos(t / T * π))$ 其中，lr_min和lr_max分别表示学习率的最小值和最大值，T表示一个周期的总批次数。

余弦退火的优点是可以在训练过程中多次降低和提高学习率，帮助模型逃离局部最优，并在不同的学习率下探索更广泛的参数空间。

StepLR：

StepLR是一种分段常数衰减的学习率调度策略。它按照预定的步长（step size）来降低学习率。

具体来说，在每个步长结束时，学习率乘以一个衰减因子（decay factor）。衰减因子通常设置为一个小于1的常数，如0.1或0.5。

例如，如果初始学习率为0.1，步长为30个epoch，衰减因子为0.1，则学习率在第30、60、90个epoch时分别降低为0.01、0.001、0.0001。

StepLR的优点是简单易实现，并且在一些任务中可以有效地帮助模型收敛。缺点是变化太突然。

Motivation：不同的参数应该用不同的学习率。

AdaGrad的公式为: $\theta_{t+1}=\theta_t-\frac{\gamma}{\sqrt{s_t}+\varepsilon} g_t$

其中, $s_t=s_{t-1}+g_t^2$ 代表着历史中所有梯度的平方和; $\varepsilon$ 是一个极小量, 防止除零。这样做的好处是可以减小之前震荡过大的参数的学习率, 增大更新速率较慢的参数的学习率, 从而让模型可以更快收敛。

RMSProp（Root Mean Square Propagation）

AdaGrad算法存在一个明显的问题, 就是它要考虑所有的历史数据, 这样就会导致 $s_t$ 越来越大,学习率的分母变大了, 也就会导致学习率越来越小, 模型收玫的速度也就会变慢了。

解决这个问题的方法还是采用指数加权移动平均法, 减小更早的梯度对当前学习率的影响, 而 AdaGrad+指数加权移动平均法就是RMSProp方法了, 其公式为: $\theta_{t+1}=\theta_t-\frac{\gamma}{\sqrt{s_t}+\varepsilon} g_t$

其中, $s_t=\alpha s_{t-1}+(1-\alpha) g_t^2$ 代表着历史中所有梯度的平方和， $\alpha$ 代表指数加权移动平均法的参数。

Adam（Adaptive Moment Estimation）

SGD算法主要在优化梯度（动量）问题, RMSProp方法在优化学习率问题，SGDMomentum+RMSProp结合起来的方法就是Adam算法了, 其公式如下:

\[\theta_{t+1}=\theta_t-\frac{\gamma}{\sqrt{s_t}+\varepsilon} v_t\]

其中, $s_t=\beta_2 s_{t-1}+\left(1-\beta_2\right) g_t^2 ;\ v_t=\beta_1 v_{t-1}+\left(1-\beta_1\right) g_t$ 。

Adam with L2 regularization（AMSGrad）算法的Pytorch实现⁴如下：

v2-c6328c23ffc6fa9b97c7a9beb4c46fba_1440w

这里注意两个地方：

这里g(t)首先是应用来一个L2范数加在g_t上，这是Adam的改进过程。
amsgrad只需要修改一个参数就可以从Adam改进过来

Adam 与二阶优化的关系

RMSProp 和 ADAM 是利用一阶梯度信息对如牛顿法的二阶优化算法的近似模拟。⁵

AMSGrad（Adam with Max Stabilization）

momentum的估计不是通过移动平均来计算的，而是通过记录最大值。

AdamW（Adam with Weight Decay）

理论上更优的原生Adam算法，有时表现并不如SGD momentum好，尤其是在模型泛化性上。

因此加上L2正则项，即Adam with L2 regularization:

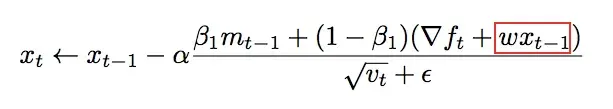
v2-3b3259beb0d638ffd10f35766e5c3684_1440w

AdamW对这个问题的改进就是将权重衰减和Adam算法解耦，让权重衰减的梯度单独去更新参数，改动点如下图所示：

v2-396940aadf6317db21cd26c90b44003e_1440w

绿色部分是AdamW改动的地方，红色的部分是Adam原有的运算过程。

AdamW算法是目前最热门的优化器，包括LLama2等大模型训练都采用的是AdamW。

Reference

https://pytorch.org/docs/stable/generated/torch.optim.SGD.html ↩
On the importance of initialization and momentum in deep learning. http://www.cs.toronto.edu/%7Ehinton/absps/momentum.pdf ↩
十分钟速通优化器原理，通俗易懂（从SGD到AdamW）. https://zhuanlan.zhihu.com/p/686410423 ↩
https://pytorch.org/docs/stable/generated/torch.optim.Adam.html#torch.optim.Adam ↩
ADAM与二阶优化算法的联系. https://www.zhihu.com/tardis/zm/art/486077289?source_id=1003 ↩

Optimizer Cookbook

SGD