[TOC]
EMNLP 23 best paper
Abstract
In-context learning (ICL) : promising capability of large language models (LLMs) by providing them with demonstration exam- ples to perform diverse tasks,即通过·提供给大模型实例来提升大模型能力
insight(假设):label words in the demonstration examples function as anchors:
1)semantic information aggregates into label word representations during the shallow compu- tation layers’ processing
2)the consolidated information in label words serves as a reference for LLMs’ final predictions
即语义在浅层聚合到anchor word上,在深层用于final prediction
提出了三种东西:
- anchor re-weighting method to improve ICL performance(ICL提升手段)
- demonstration compression technique to expedite inference(推理加速)
- analysis framework for diagnosing ICL errors in GPT2-XL(错误诊断方法)
Intro
两个假设:
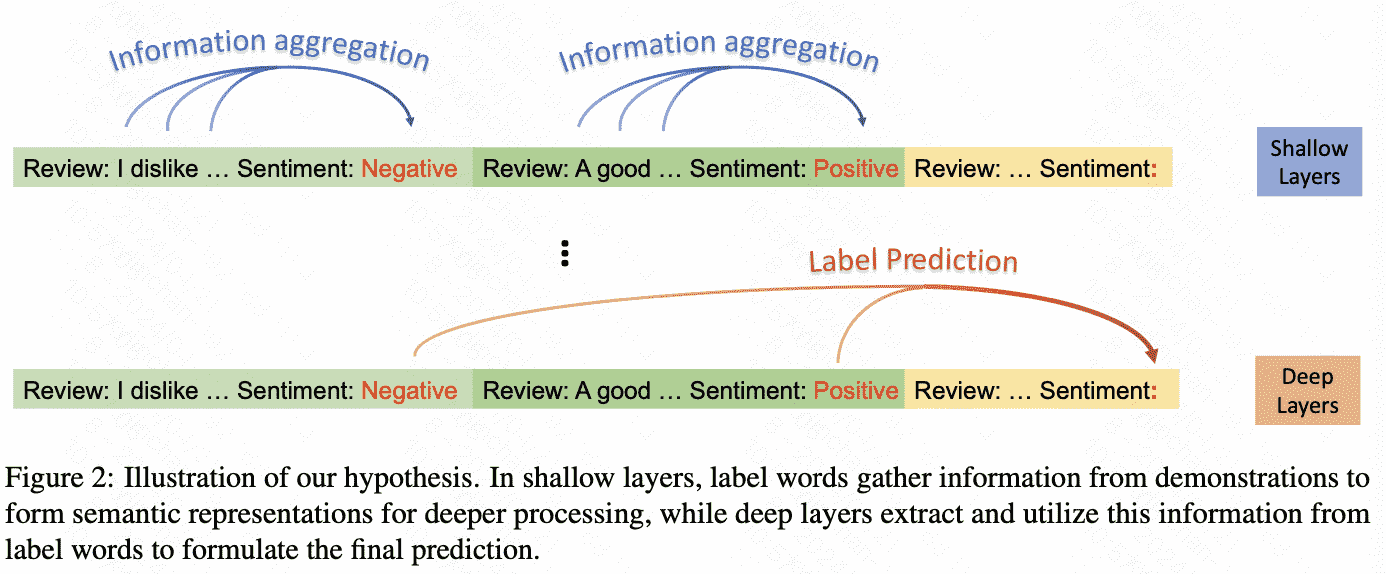
- 在浅层中,标签词收集示例的信息,形成深层的语义表示。
- 在深层中,模型从标签词中提取信息以形成最终预测。

根据假设,可以给上图的注意力这样的解释:
Verifying the Hypothesis
Metrics
- 显著性得分矩阵:
$A_{h, l}$ 是第 1 层中第 $\mathrm{h}$ 个注意力头的注意力矩阵的值, $x$ 是输入, $L(x)$ 是任务的损失函数. $I_l(i, j)$ 代表上下文学习中从第 $\mathrm{j}$ 个字到第 $\mathrm{i}$ 个字的信息流的显著性性。
- 三个信息流指标:
$S_{w p}$, the mean significance of information flow from the text part to label words: \(\begin{aligned} S_{w p} & =\frac{\sum_{(i, j) \in C_{w p}} I_l(i, j)}{\left|C_{w p}\right|}, \\ C_{w p} & =\left\{\left(p_k, j\right): k \in[1, C], j<p_k\right\} . \end{aligned}\) $\boldsymbol{S}{p q}$, the mean significance of information flow from label words to the target position: \(\begin{aligned} S_{p q} & =\frac{\sum_{(i, j) \in C_{p q}} I_l(i, j)}{\left|C_{p q}\right|}, \\ C_{p q} & =\left\{\left(q, p_k\right): k \in[1, C]\right\} . \end{aligned}\) $\boldsymbol{S}{w w}$, the mean significance of the information flow amongst all words, excluding influences represented by $\boldsymbol{S}{w p}$ and $\boldsymbol{S}{p q}$ : \(\begin{aligned} S_{w w} & =\frac{\sum_{(i, j) \in C_{w w}} I_l(i, j)}{\left|C_{w w}\right|}, \\ C_{w w} & =\{(i, j): j<i\}-C_{w p}-C_{p q} . \end{aligned}\)
可以看到浅层数据流从text part to label words,深层从label words to the target position:
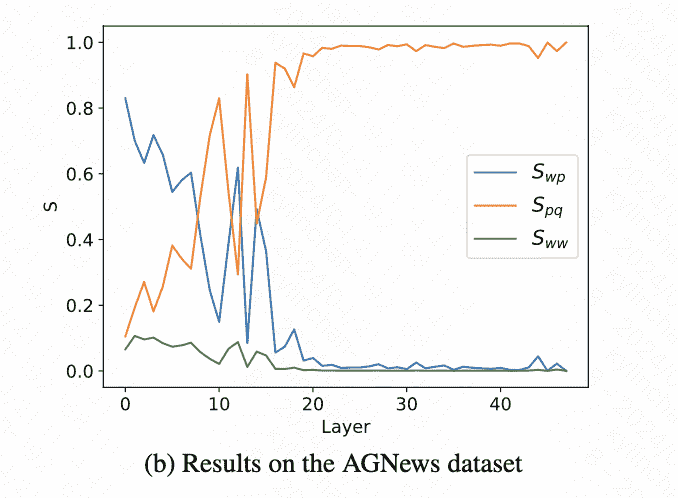
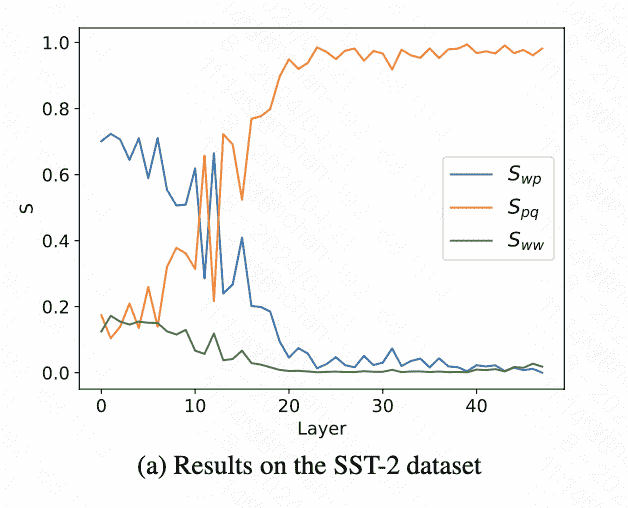
Shadow Layer:词隔离
为了作证猜想一:随后作者又通过操纵注意力矩阵A来隔离标签词, 从而阻断标签词的信息流。详细来说就是将特定层数的注意力矩阵中标签词和标签词之前的词的注意力元素置为 0 : \(A_l(p, i)(i<p)=0 \text { 。 }\)
作者使用以下指标来评估阻止从文本部分到标签标记的信息流的影响:(1) 标签忠诚度:测量有隔离和无隔离的输出标签的一致性。(2) 单词忠诚度:使用Jaccard similarity来比较前5个预测单词隔离和不隔离的相似度, 捕捉更微妙的模型输出变化。忠诚度低表明孤立对模型预测影响更大。
通过实验作者绘制了下图:
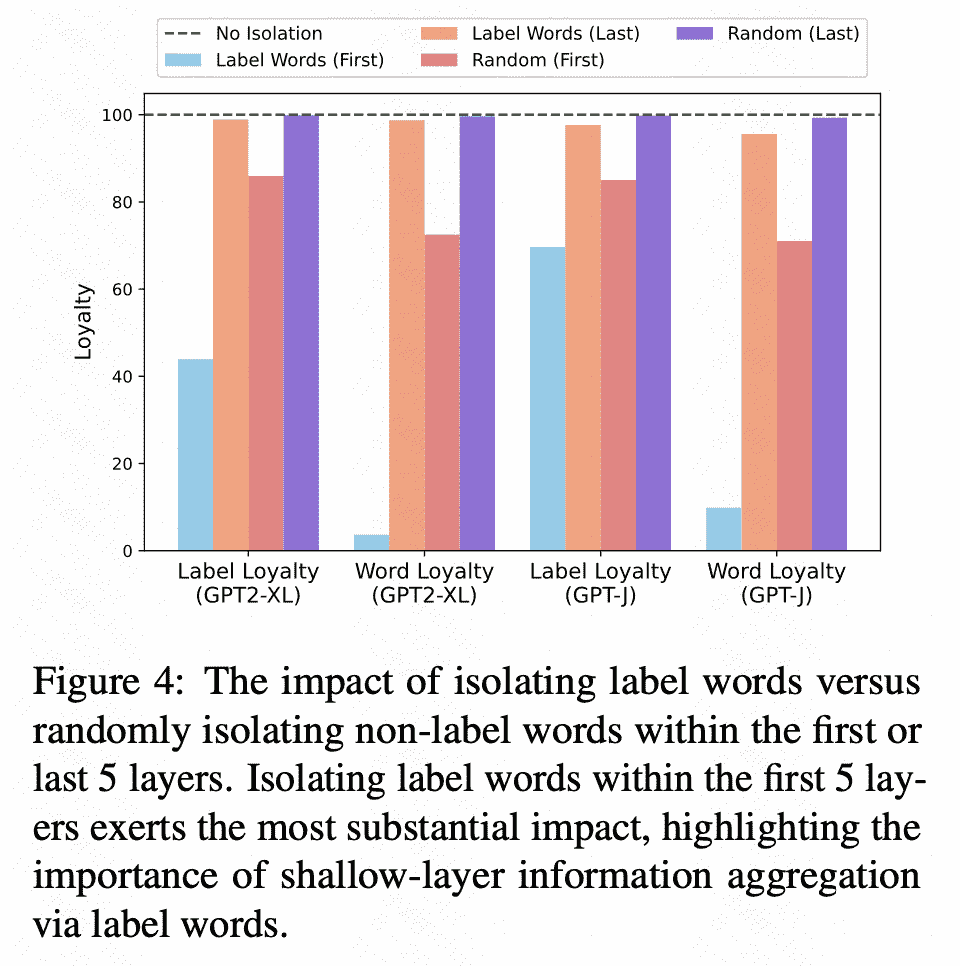
Deep Layer:Attention数据对预测贡献度
文章利用AUC-ROC评分来量化 $A_l\left(q, p_i\right)$ 和模型预测之间的相关性. 考虑到transformer的残差机制, 作者可以将每一层的隐藏状态视为所有先前层计算的累积效应,提出了 $R_l$ ,用来量化前 $\mid$ 层对模型预测的累积贡献 \(R_l=\frac{\sum_{i=1}^l\left(\mathrm{AUCROC}_i-0.5\right)}{\sum_{i=1}^N\left(\mathrm{AUCROC}_i-0.5\right)} .\)
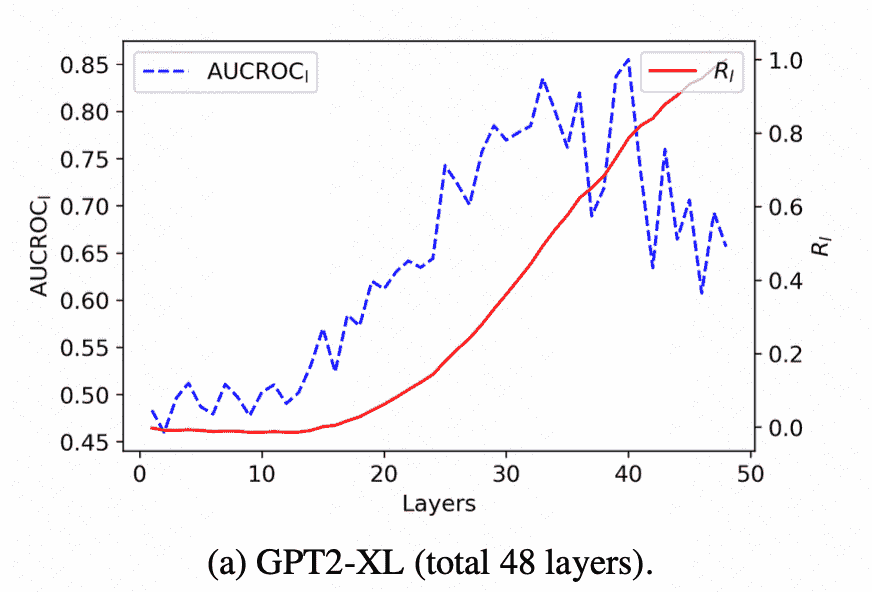
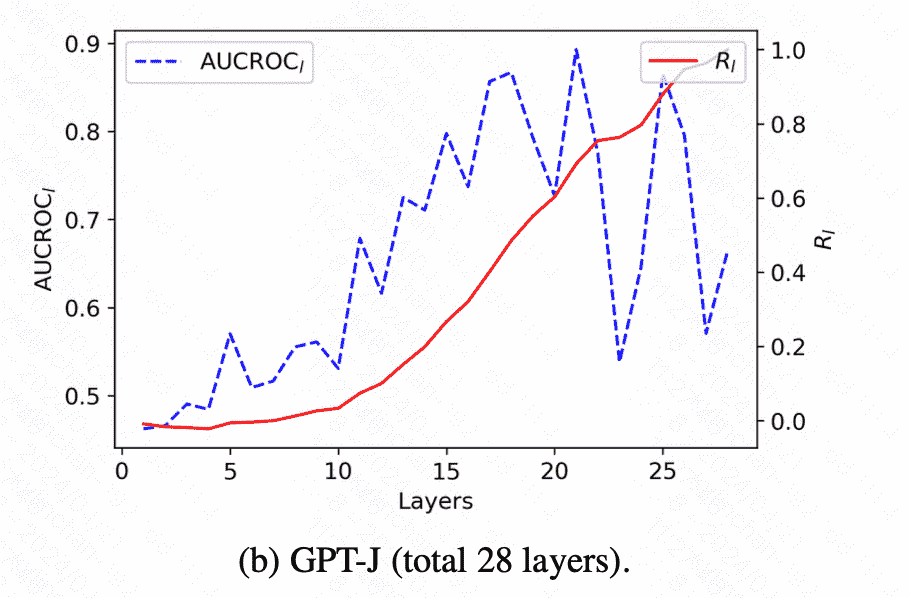
结果表明了深层对最终预测的关键作用,验证了该模型从深层的标签词中提取信息以形成最终预测。
Application
Anchor Re-weighting
在每层的每个注意力头前都乘上一个可学习的参数 $\beta$, 然后在训练集上对 $\beta$ 进行更新 \(\hat{A}\left(q, p_i\right)=\exp \left(\beta_0^i\right) A\left(q, p_i\right)\) \(\boldsymbol{\beta}^{\star}=\arg \min _{\boldsymbol{\beta}} \mathcal{L}\left(\boldsymbol{X}_{\text {train }}, \boldsymbol{Y}_{\text {train }}\right)\)
Anchor-Only Context Compression
具体的做法是: 计算和缓存示例中的标签词隐藏状态 $H=\left{\left{h_l^i\right}{i=1}^C\right}{l=1}^N \quad\left(h_l^i\right.$ 是示例中第 $\mathrm{i}$ 个标签词的第 $\mathrm{I}$ 层隐藏状态)。在推理过程中, 通过在每一层的前面串联 $h_l^1, \ldots, h_l^C$, 而不是使用完整的示例, 可以加快推理速度。
Anchor Distances for Error Diagnosis
最后, 文章通过检查注意力模块中与标签词相对应的key向量之间的距离, 对ICL进行了误差分析。
由前文的分析, 作者认为如果标签词pi和pk的key向量k相似, 那么A(q, pi)和A(q, pk)也可能相似,这可能导致标签混淆。另外, 考虑到查询向量 $q_q$ 的分布, 作者使用类PCA方法提取key向量沿 $q_q$变化显著方向的分量: $\hat{k}$ (详见附录J)。作者认为这些 $\hat{k}$ 之间的距离可以对应模型的类别混淆,是ICL错误的一个可能来源。因此, 作者将距离标准化为 $0-1$ 的尺度, 其中 0 表示最高程度的类别混淆。